- Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- Wireless ConnectivityWireless Connectivity
- RFID / NFCRFID / NFC
- Advanced AnalogAdvanced Analog
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Digital Signal Controllers
- Vybrid Processors
- ColdFire/68K Microcontrollers and Processors
- 8-bit Microcontrollers
- PowerQUICC Processors
- OSBDM and TBDML
- S32M
-
- Solution Forums
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
-
- Cloud Lab Forums
-
- Knowledge Bases
- ARM Microcontrollers
- Identification and Security
- i.MX Processors
- Model-Based Design Toolbox (MBDT)
- QorIQ Processing Platforms
- S32 Automotive Processing Platform
- CodeWarrior
- Wireless Connectivity
- MCUXpresso Suite of Software and Tools
- MQX Software Solutions
- RFID / NFC
- Advanced Analog
-
- Home
- :
- 基于模型的设计工具箱(MBDT)
- :
- 基于模型的设计工具箱(MBDT)
- :
- Re: Module 7: Torque Control
Module 7: Torque Control
Module 7: Torque Control
|
EV Powertrain source: carmagazine.co.uk |
INTRODUCTION
Nowadays, are we witnessing the start of a global revolution within the automotive industry, where more and more car manufacturers are trying to compete in the rising sector of electrical vehicles. At the core of this revolution sits the "work horse" of modern transportation: the humble electric motor.
In this module of the 3-Phase PMSM Control Workshop with NXP's Model-Based Design Toolbox , we are going to discuss about the FOC for traction motors and how to control the torque produced by PMSM. The control method is generic and may be applicable to all sort of means of transportation: trains, buses, bikes, scooters and modern day cars.
In a car with internal combustion engine each time you press the gas pedal, the throttle valves open, more fuel and air is injected into cylinders resulting in a stronger explosion that sends the piston down with a stronger force. This linear force pointed downward is converted via the crankshaft into a rotational movement with a certain amount of torque given by the product between the force and rod length. Therefore, each time you press the "pedal to the metal" you control an amount of torque the engine is capable of. Under normal driving conditions the speed of the vehicle is regulated in driver's head that ultimately decides to push the acceleration pedal more or less.
The purpose of this article is to replicate such control system. The user will be able to set a torque reference and the motor will obey that command speeding up or slowing down based on how much torque is being demanded. In this module we are going to learn how to:
- Implement FOC by closing the current loop with the values read from ADC;
- Regulate the Torque and Flux in (dq) coordinate system with standard PI controllers;
- Use Park transformations to liniarize the control quantities;
- Synchronize the SLOW and FAST control loops with the ADC interrupts;
- Start-up the PMSM from a well known position;
- Configure the motor and drive protections;
In Fig. 1, which represent the global application mapping diagram as discussed in Module 3: System Partitioning , are shown the new hardware blocks that are going to be configured and used to perform the PMSM FOC Torque Control highlighted in green relative to the ones already configured so far in the previous modules of this workshop. We are going to reuse and enhance the model developed in Module 6: Current Sensing (Part 1/2) and Module 6: Current Sensing (Part 2/2) which will allow us to test the application in real time on S32K144 3-phase PMSM Development Kit|NXP . The interactions between host PC and hardware will be done via OpenSDA serial communication that will be used to download the code generated from MATLAB and to visualize various control signals with FreeMASTER. In addition, the user can start and control the motor speed from the SW2 and SW3 push button present on the S32K144 Evaluation Board|NXP . A three color LED will be used to signal the control states and faults.
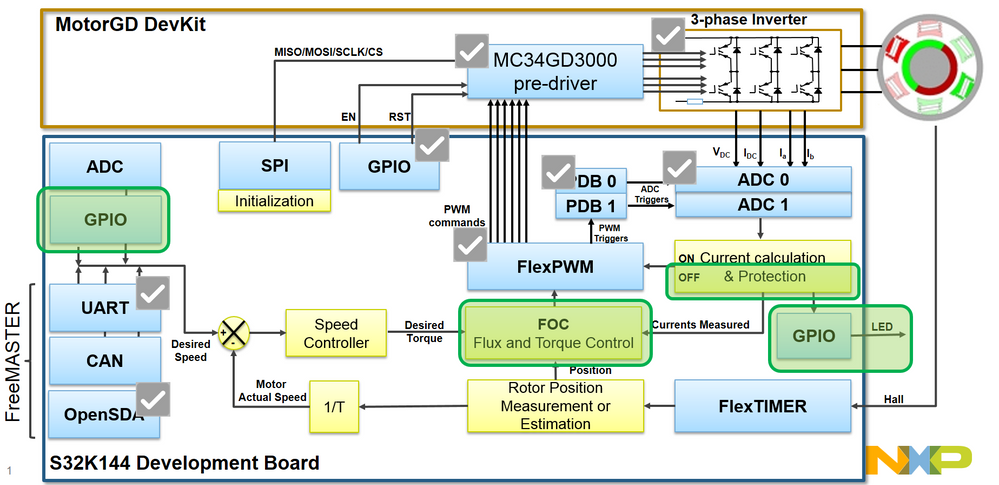 |
| Fig. 1: Application Mapping - new HW & SW modules used for FOC Torque Control are highlighted in green |
TORQUE CONTROL
The Torque Control replicates the behavior of internal combustion engine. As is was explained in Module 2: PMSM and FOC Theory to achieve the adequate motor response we need to:
- maintain 90 electrical degrees angle between Torque and Flux axis by regulating the currents in Q and D axis.
- maximize the PMSM torque that is proportional with the stator current vector projection on the Q axis.
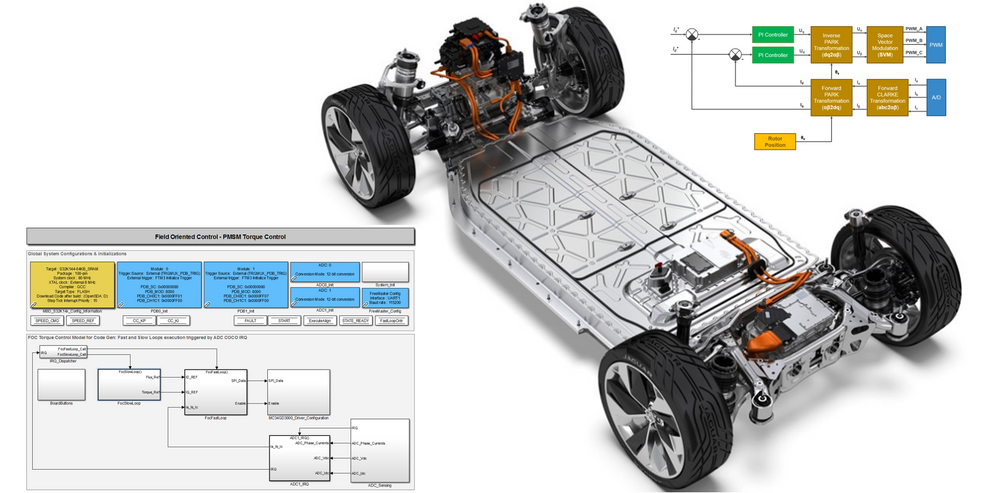
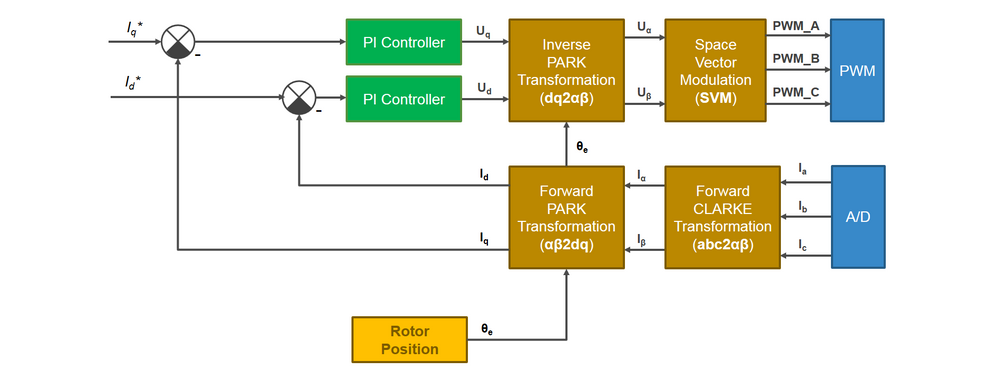
In Fig. 2, is shown the block diagram of the Torque Control system proposed for implementation. The Field Oriented Control is executed in the FAST CONTROL LOOP block that is executed based on a ADC trigger at each 100 microseconds. This subsystem receives the references values for currents in Q (torque) and D (flux) axis and the currents measured from the ADC and outputs the PWM duty cycles commands that controls the 3-phase inverter.
The toque and flux references are computed in the SLOW CONTROL LOOP block that is triggered at each 1 milisecond based on the same ADC events as the FAST CONTROL LOOP. The speed and torque commands are received via the UART or from on board push buttons and transformed based on a LUT into actual torque and electric angle increments.
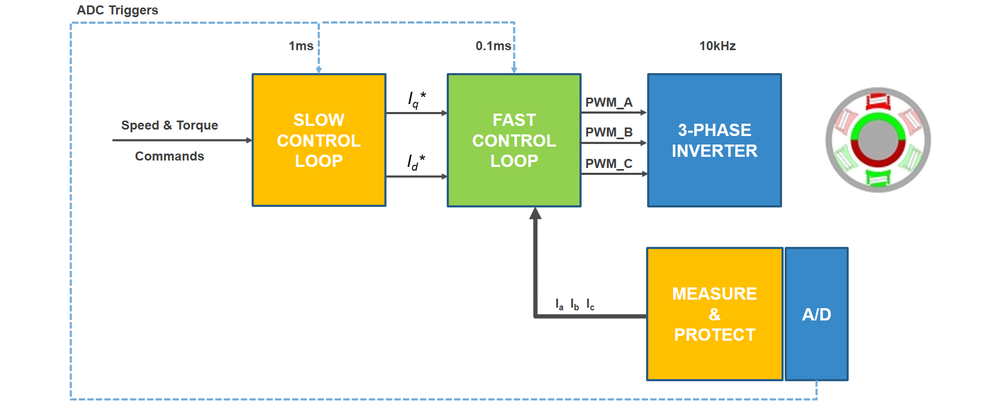 |
| Fig. 2: FOC Torque Control - Block Diagram |
As you can see in Fig. 2, we have only one loop that is closed: current loop. The outer speed loop is still open, hence it does not prevent us for implementing the torque control even if this is not ideal. The outer speed loop will be closed in the next module of this workshop.
SLOW CONTROL LOOP
The block diagram of the functions implemented on SLOW CONTROL LOOP is shown in Fig. 3. At each startup, a special alignment sequence is executed in order to move the PMSM rotor into a particular well known position - rotor magnetic D axis is align with PMSM stator phase A. The rotor alignment is a key aspect in torque control since we want to produce the highest torque available and that can only be done if we maintain a 90 electrical degrees between Q axis and rotor magnetic flux axis D
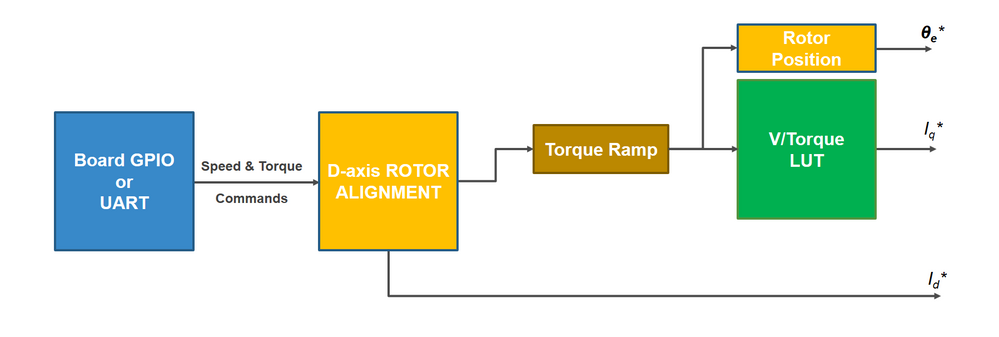 |
| Fig. 3: Slow Control Loop - Block diagram for Torque Control |
The alignment is achieved by injecting a current into the D-axis, forcing this way the rotor magnets to align with the magnetic field produced in the stator. For the rotor alignment we need two parameters:
- the magnitude of the current in the D-axis, which depending on the load it should be closed to the motor rated current or even a bit higher;
- alignment time that gives the time period while the current is maintained thru stator coils ensuring the rotor is being dragged into the correct position;
Once the rotor alignment is completed the speed command is transformed into the torque command via a LUT similar with the method from Module 5: V/F Scalar Control
In the same time with torque reference computation, the actual electric angle increment is computed in order to rotate the motor.
FAST CONTROL LOOP
The block diagram of the functions implemented on FAST CONTROL LOOP is shown in Fig. 4. As it can be noticed this is the complete diagram of the Field Oriented Control as discussed in Module 3: System Partitioning
 |
| Fig. 4: Fast Control Loop - Block diagram for Torque Control |
Based on the reference input values of Torque (Iq), Flux (Id) and the PMSM measured phased currents, after PARK forward transformation the appropriate control voltages for (dq) reference system are computed with the help of two independent PI current controllers. Once the command voltages are obtained, the inverse PARK and CLARKE transformations are used to compute the PWM duty factors via the Space Vector Modulation technique to control the 3-phase inverter MOSFETs.
The theory behind the PI controllers was discussed in Motor Control Class: Lecture 11 - Closed Loop Control
In case of motor electric transfer function the procedure of computing the current controller Kp and Ki gains is the same as the one presented for the speed controller with the observation that Inertia (J) is replaced with Inductance (L) and Friction coefficient (b) is replaced with Resistance (R). The rest of the computations remains similar.
Note, how in the Fig. 4, we are demanding the rotor to move in a desired position based on the computation of the electrical angle (theta) that is derived from the speed reference computed in SLOW CONTROL LOOP. Since there is no loading torque on the motor, we are going to use for demonstration this method of controlling the motor torque in open loop since it is safe and will produce good results. In case there is a loading torque and the rotor alignment is not correct the motor might lose the synchronism and will stall. For such cases you will need:
- actual rotor position sensor (we will address that in M8)
- estimate the rotor position based on measurements and mathematical model (we will address that in M9)
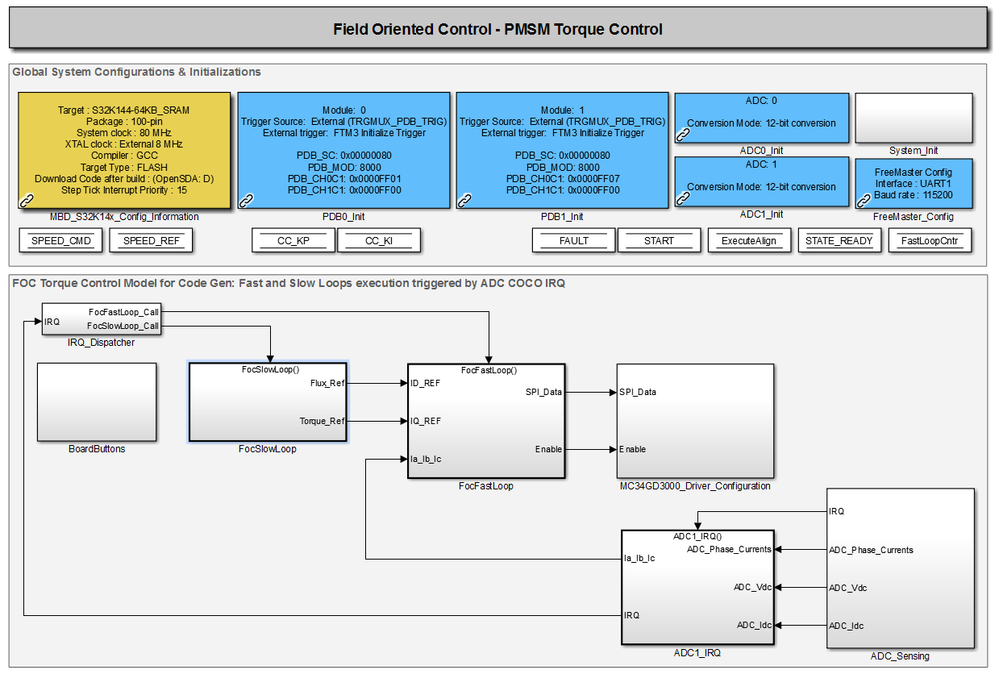
The Simulink model used to implement all these functionalities is shown in Fig. 5:
 |
| Fig. 5: Simulink model for PMSM FOC Torque Control |
| Video training: How To Implement and Test Torque Control System for PMSM Using S32K144EVB | ||
|---|---|---|
Please watch this video before going further. The rest of the article is a summary of the video.
TORQUE CONTROL SIMULINK MODEL
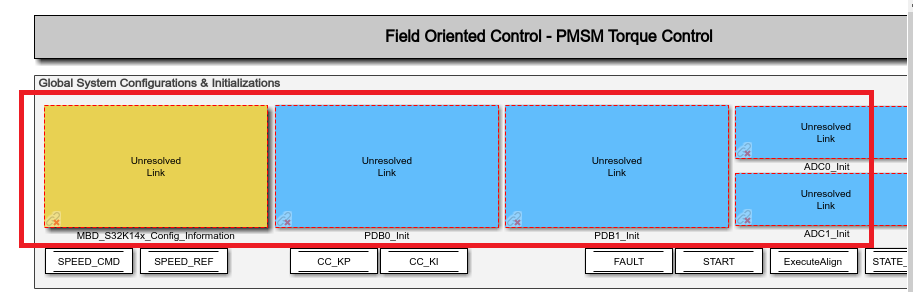
In this section we are going thru the high level details regarding the implementation of Toque Control model shown in Fig. 5. The model is available for download at the end of the article. In the figures below we are going to discuss only new functionalities added or changed compared to the model implemented in Module 6: Current Sensing (Part 1/2)
ADC Interrupts
Since we need the FOC software routines (SLOW CONTROL LOOP & FAST CONTROL LOOP) to be synchronized with the ADC measurements as it was shown in Fig. 9 from Module 6: Current Sensing (Part 1/2) we are going to modify the PDB1_IRQ to trigger a function call based on ADC conversion complete (COCO) interrupt that corresponds to the AD15 - PMSM Phase B current. For this we are going to use the ADC_ISR block that allows us to read the conversion results and trigger an interrupt in the same time.
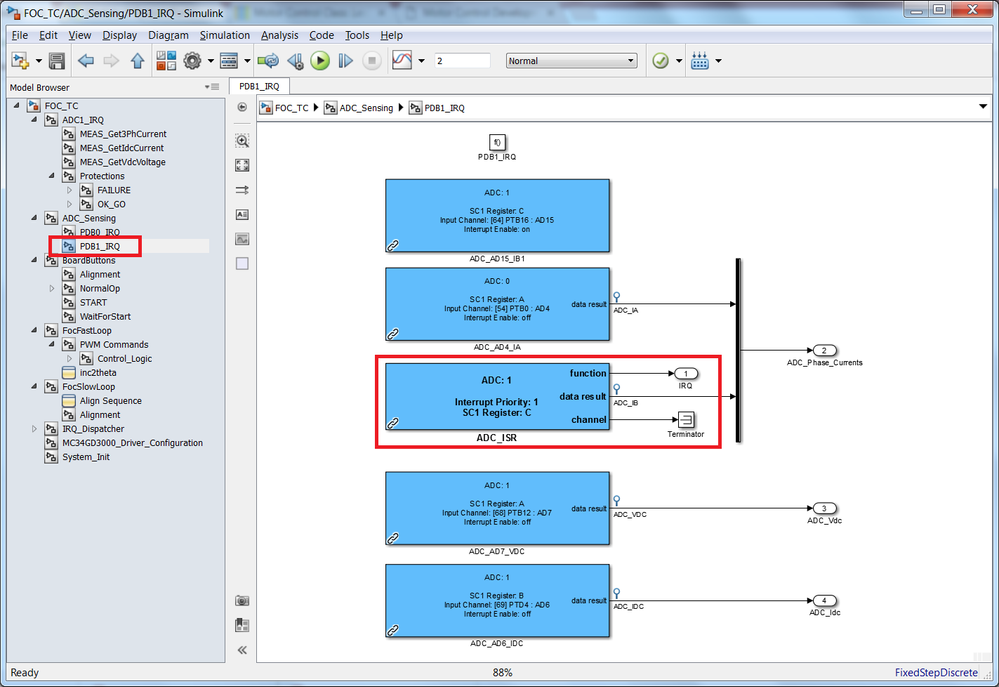 |
| Fig. 6: ADC Interrupt trigger for SLOW and FAST Control Loops |
Interrupt Dispatcher
Because the ADC interrupts are synchronized with the PWM frequency, it means that we will get an interrupt at each 100 micro-seconds for a 10kHz switching frequency. That is OK for the FAST CONTROL LOOP which we want to be triggered at each 100 micro-seconds, but for the SLOW CONTROL LOOP that must be scheduled at each 1 mili-seconds we need to implement a sort of dispatching mechanism. This is done in the IRQ_Dispatcher subsystem as shown in Fig. 7.
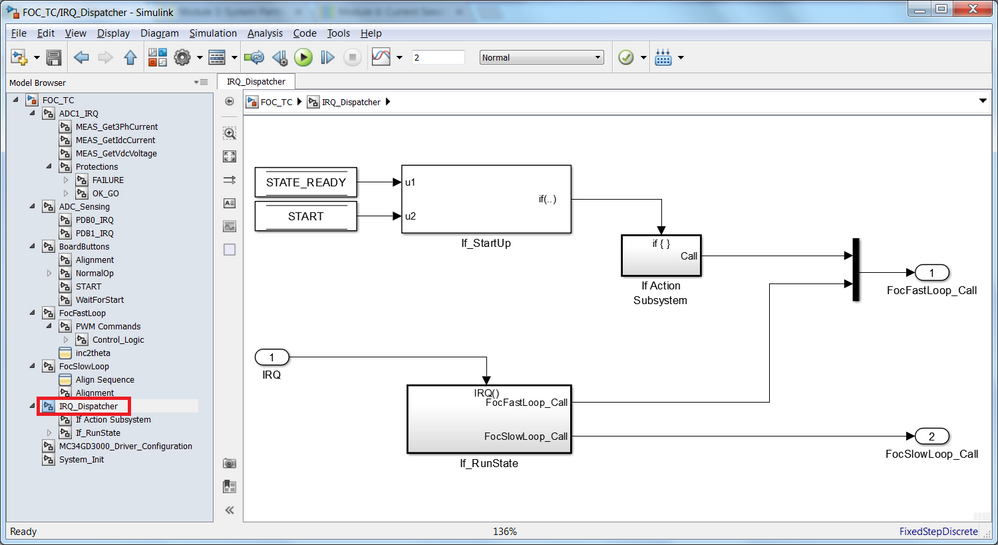 |
| Fig. 7: Dispatching interrupts to FAST and SLOW CONTROL LOOPS based on ADC HW COCO interrupt |
This block implements a two stage logic:
- StartUp sequence - when there are no ADC interrupts prior of enabling PWM but still need to execute the FAST CONTROL LOOP in order to configure the MOSFET pre-driver MC34GD3000
- normal RunState - when ADC interrupts are active and we need to delay the triggers for the SLOW CONTROL LOOP leaving unchanged the timings for the FAST CONTROL LOOP in order to insure the 10:1 execution rate between FAST vs. SLOW loops.
The dispatching mechanism that keeps a relative execution rate of 10:1 is implemented as:
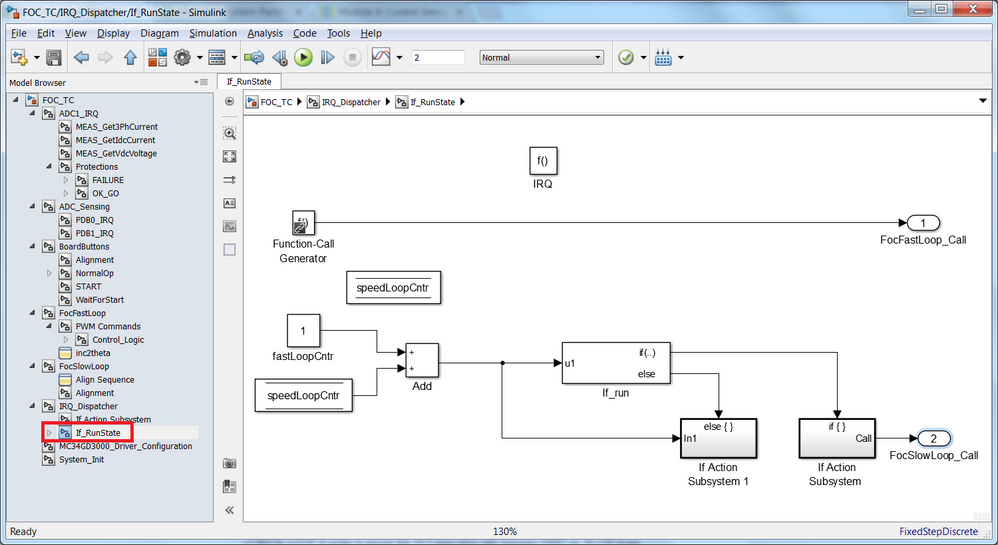 |
| Fig. 8: Interrupt dispatcher implementation for execution rate 10:1 between FAST vs. SLOW loops |
Slow Control Loop
This subsystem was modified as shown in Fig. 9, to allow:
- rotor alignment during the startup sequence. This procedure is using an AlignTimer to count how many seconds the rotor should be kept under alignment.
- speed to torque transformation via a dedicated LUT
As Fig. 9 shows, we have kept the same mechanism used for Module 5: V/F Scalar Control to generate the electrical angle profile and the the references for the (dq) system commands.
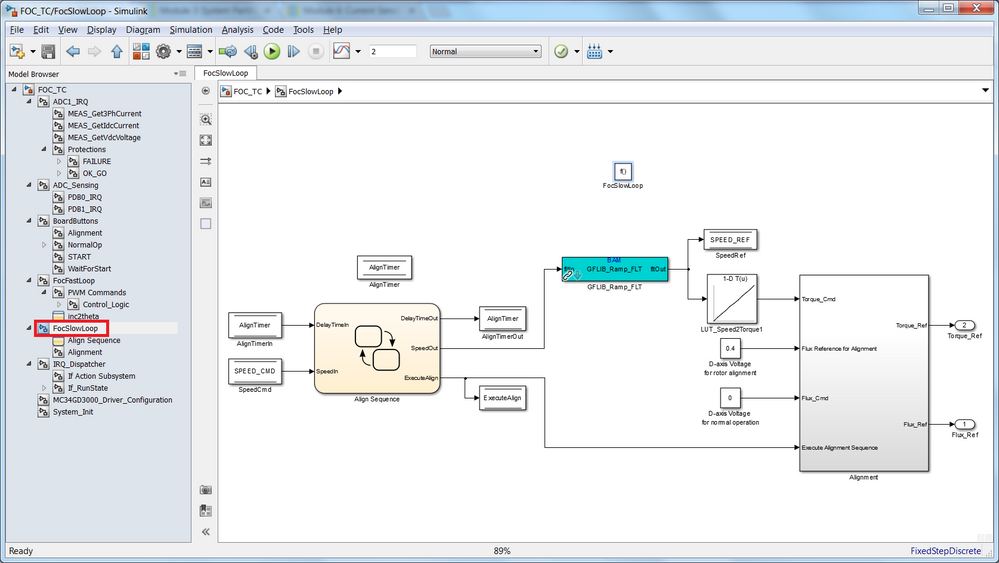 |
| Fig. 9: SLOW CONTROL LOOP implementation |
Fast Control Loop
This subsystem was enhanced with two PI controllers for each of (dq) axis and the forward PARK and CLARKE transformations that are now used to compute the currents in (dq) reference system starting from the values measured from ADC.
As can be noticed, during the alignment process the PI controllers are bypassed while the commands from SLOW CONTROL LOOP are directly applied as voltage commands to the FOC transformations. This ensure a faster and stronger response, forcing the rotor to align more precisely into the correct positions without additional delays cause by the PI controllers.
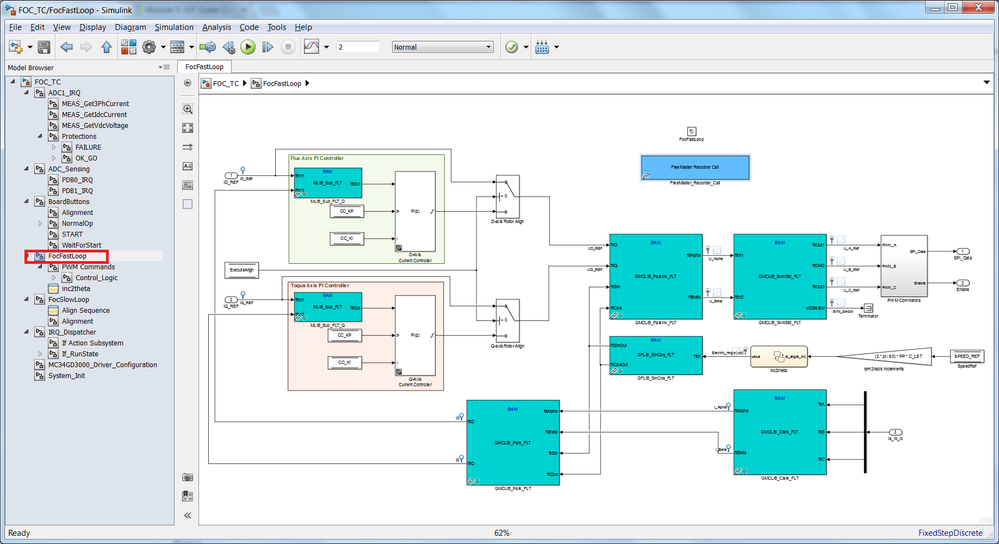 |
| Fig. 10: FAST CONTROL LOOP implementation |
Board Controls
The subsystem shown in Fig. 11, implements the logic of reading the push buttons from the S32K144 Evaluation Board|NXP that allows us to change the motor speed manually and the mechanism of LED notification. The LED logic is implemented as:
- after reset the GREEN LED is ON signaling the application is ready for receiving commands;
- during the alignment the GREEN LED is toggling;
- during normal operation the BLUE LED is ON signaling the application is operating normally;
- if a fault occurs the RED LED is ON and the motor will stop automatically. The only way to get out of this state is by pressing the RESET button;
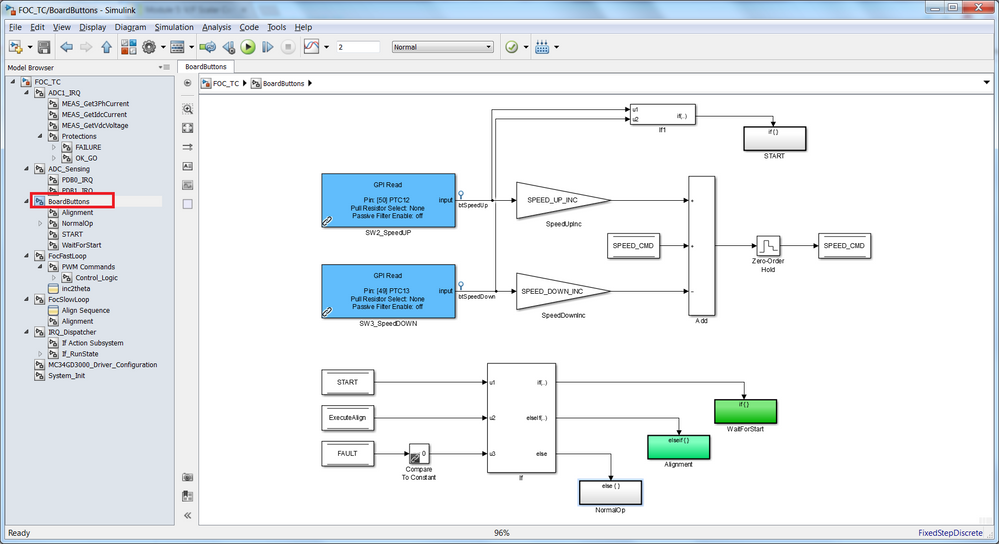 |
| Fig. 11: I/O board controls |
Protections
The motor and drive protections are implemented in the ADC interrupt routine immediately after the measurements in order to make sure that any fault is addressed as soon as possible. Currently there are three protections implemented but in next modules, additional ones will be added:
- under-voltage protection if the DC bus voltage is below 8V;
- over-voltage protection if the DC bus voltage is above 18V;
- DC link over current if the value of the current on DC link exceeds 4A;
If one of these conditions occurs the application will disable the PWM generation immediately and the application will not be able to be resumed until a RESET is issued by the user.
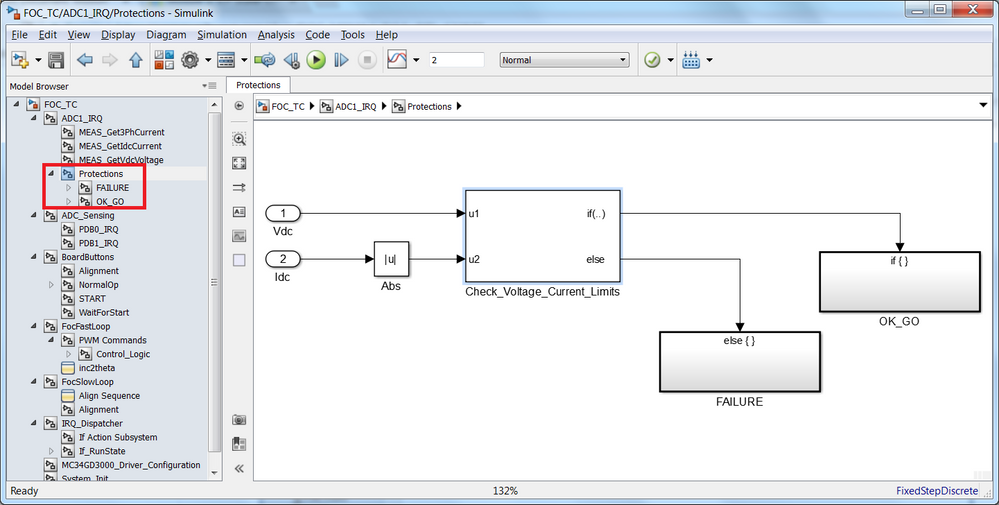 |
| Fig. 12: Protections |
EXPERIMENTAL RESULTS
Using the FreeMASTER attached project we can check the system responses and tune the controllers to responds however we wish on the fly in real time. For demonstration purposes the controller are de-tuned in order to increase the respond time and have easy to understand pictures.
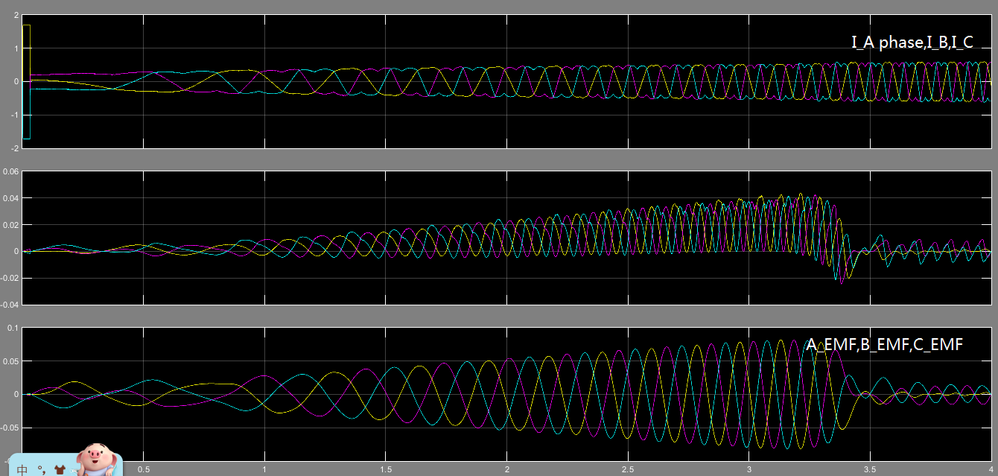
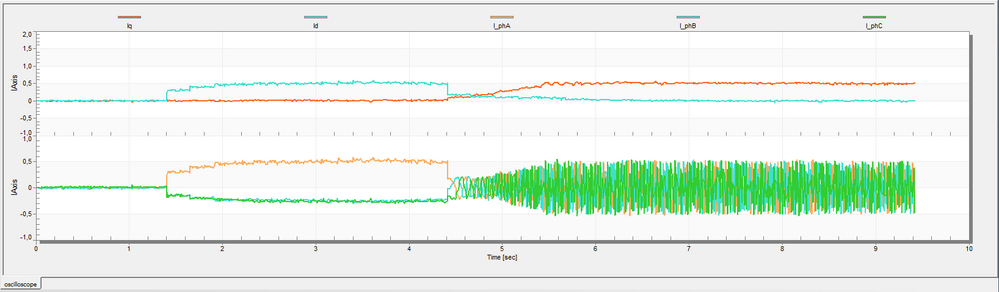
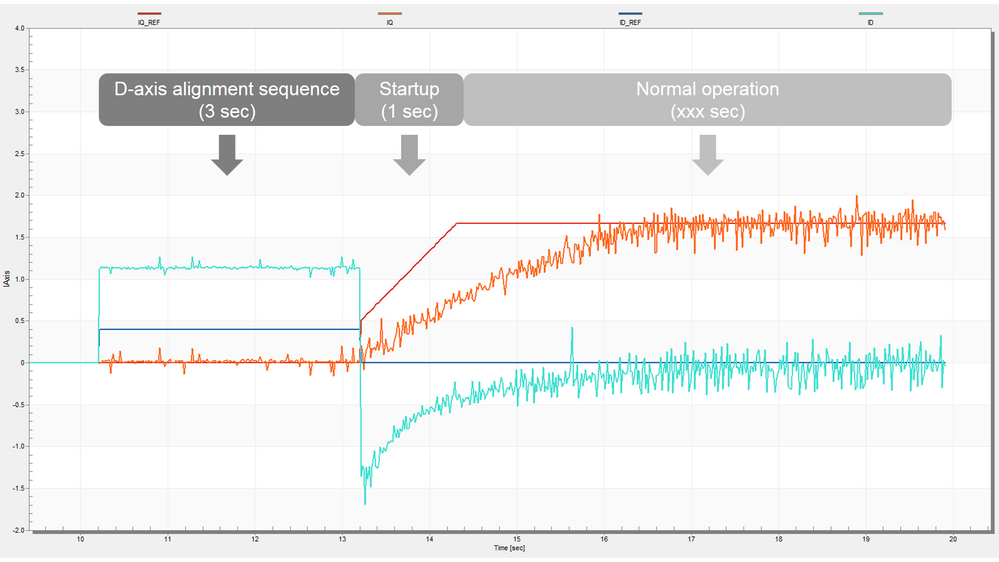
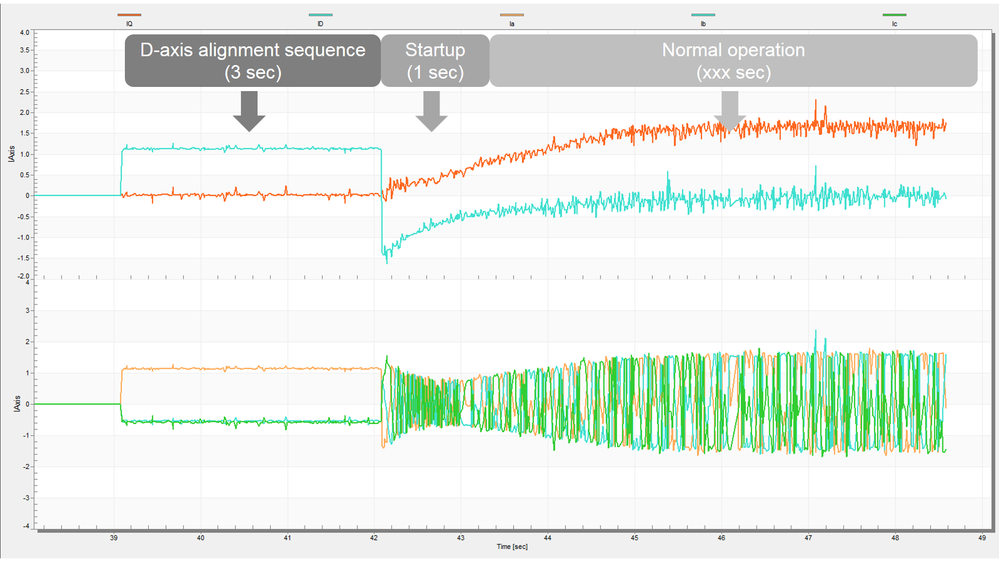
Fig. 13, shows the system response during the alignment sequence, startup and normal operation. You can see that the alignment sequence is lasting for 3 seconds. In this time interval ~1.1 amps are injected in the flux axis in order to force the motor alignment with stator phase A. The correspondence between the (dq) currents and the actual (abc) currents can be clearly observed in Fig. 14.
 |
|
Fig. 13: Startup sequence: alignment, startup and normal operation showing: - Torque reference (IQ_REF - red) and Actual Torque (IQ - orange) - Flux reference (ID_REF - blue) and Actual Flux (ID - cyan) |
 |
|
Fig. 14: Startup sequence: alignment, rump-up and normal operation comparison between the (dq) reference system and (abc) reference system - Actual Torque (IQ - orange) and Flux Flux (ID - cyan) in the upper part - Actual PMSM phase current Ia, Ib, Ic |
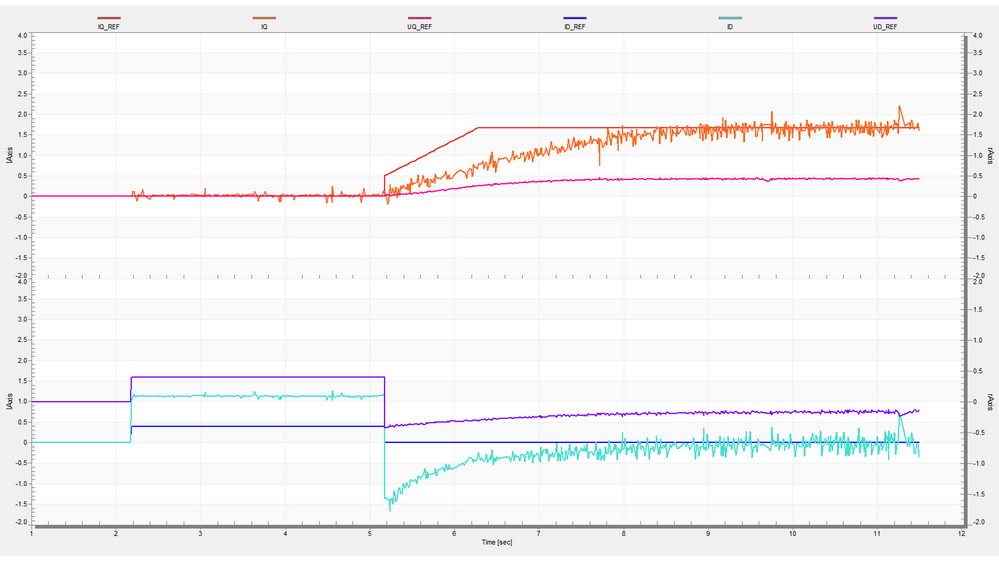
Fig. 15, shows the PI controllers responses during startup and normal operation. As you can see in order to maintain almost 1.5 amps thru the motor we need only a small amount of control voltage (0.5 volts - on the right axis).
 |
|
Fig. 15: PI Current Controller behavior: inputs vs outputs - Torque axis response (upper) - Flux axis response (lower) |
Fig. 15, shows that there is plenty of room to play of current controller tuning parameters and improve the system response since the voltage reserve is not reached.
How would you tune the current controllers ? Do you prefer a sharp or a mild response and why is that ?
Update revisions:
March 19, 2018
- update the M7.zip model. This Simulink model is tuned for the LINIX 45ZWN24-40 motor as part of S32K144 3-phase PMSM Development Kit|NXP
Update January 28th 2019 - This Simulink model is now available on MATLAB 2018b and MBDT for S32K14x 2018.R1 release
Before using the new models make sure you apply all the hot-patches from here: HotFix: MBD Toolbox 2018.R1 for S32K
Update revisions:
March 18, 2019
- update the model to work with Model-Based Design Toolbox for MPC57xx Automotive Version 3.0.0 .
May 06, 2020
- update the model to work with Model-Based Design Toolbox for MPC57xx Automotive Version 3.2.0 .
Hello, @Daniel_Popa @mariuslucianand
I think there is something wrong, I can't see the images and videos.
Thanks
hi,
i am using matlab R2019a. When I open FOC_TC file....I am getting warning as unable to open 'mbd_s32k14_ec_toolbox'. How to resolve it?
Hello bhanu.kassel@gmail.com,
What MBDT Toolbox are you using?
The latest version tooblox name of the mbd_s32k14_ec_toolbox.mld is now mbd_s32k_ec_toolbox.mdl. Replacing the link might help.
Marius
Hello.
i am trying to implement a Parameter estimation algorithm of the PMSM by using MATLAB functions within the torque Control model and i would like to use the 112 MHz clock Speed.
i tried changing it from 80 MHz to 112 MHz but the board goes immediatly to fault mode.
is there any additional Settings that i Need to Change to run at 112 MHz ?
Best Regards
Ali Terro
Hello Ali ´Terro,
Running the S32K144 at 112MHz assumes changing the running mode to HSRUN, which can only be performed from the RUN mode. Before that, I recommend you reading the Power Management chapter from the S32K Reference Manual.
But How do you make this transition into HSRUN? Using a PMC block or setting the HSRUN from the config block?
Best Regards,
Marius
Hellodumitru-daniel.popa
Is it possible to provide to me the same model with Matlab 2018A or 2017B version. Thanks in advance
You can change the models by yourself. Please have a look at my previous comment: https://community.nxp.com/thread/466420#comment-1106222
Hope this helps!
Daniel
Hello
I have download the "M7" model and i have the following issue:
Unresolved Link for all the blocks of S32K14x.
Refer to the following:
For your information, i have installed the MBDT for S32K 2018.R1 and i have MATLAB 2018A as version
I tried to build and download to the my board the "BLDC_OpenLoop_s32k14x.slx" model : it work fine
Could you please tell me how i can resolve this issue.
Best regards
I've updated the models to works with the latest release. Please download the new zip files marked ***2018.R1.zip. and let us know if it is working.
Best regards,
Daniel
Hello dumitru-daniel.popa
Long time no see because of delays by some things. After watching M7 I made a modification based on the M5 simulation model, added a current loop, and I had no motor so I tried to use your previous module.
The purpose of my help is because the model is still wrong. It will suddenly become unstable before the motor speed reaches 200rmp. As a result, the speed will drop sharply and the back EMF will be abnormal, but the A, B and C three-phase currents seem to be correct. I Attempts to modify the parameters of the motor model are not successful. According to your mature experience, can you give suggestions for modification?
If the motor is working, can you tell me what is the phase difference between the back-EMF and the phase current?
Should I close the speed loop with you to make the system work properly? If I change the Vdc once, the system is no longer normal and the motor parameters seem to be important.
How to select the current loop parameters?
I attached my model, thank you.
best regards!
wangxuan
Hello dumitru-daniel.popa
Am I correct that during the alignment Operation the current I_phA should be eual to I_dcb ?
I was not able to read any value with the dc link shunt and it is 0 over all the time.
I think this is because the ADC is triggered in the middle of on time of the low side igbt's.
Do you have any recommendations ?
Hi Leon,
Am I correct that during the alignment Operation the current I_phA should be eual to I_dcb ?
Not necessary. Think about what the inverter is doing ? It is basically a power source that takes as input the Vdc * Idc and outputs U*I
In case of alignment you have the current flowing thru phase A (Ia) and returning via phase B (-0.5Ia) and phase C (-0.5Ic)
If you where about to apply all the Vdc as phase voltage, then yes - the relation would be: Vdc*Idc = Ua*Ia. Since Ua will be equal to Vdc then Idc will have to be Ia.
BUT - for aligning you do not apply the entire Vdc - only a certain percentage of it since you have no BackEMF. Therefore the Ia != Idc.
Hope this helps!
Daniel
Hello Daniel,
In case of alignment you have the current flowing thru phase A (Ia) and returning via phase B (-0.5Ia) and phase C (-0.5Ic)
Exactly this you can see in this Image:
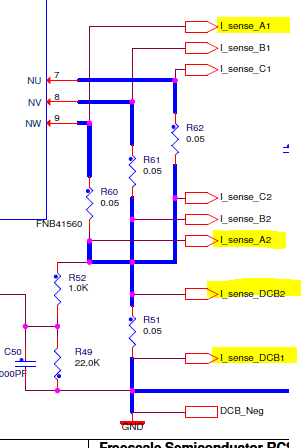
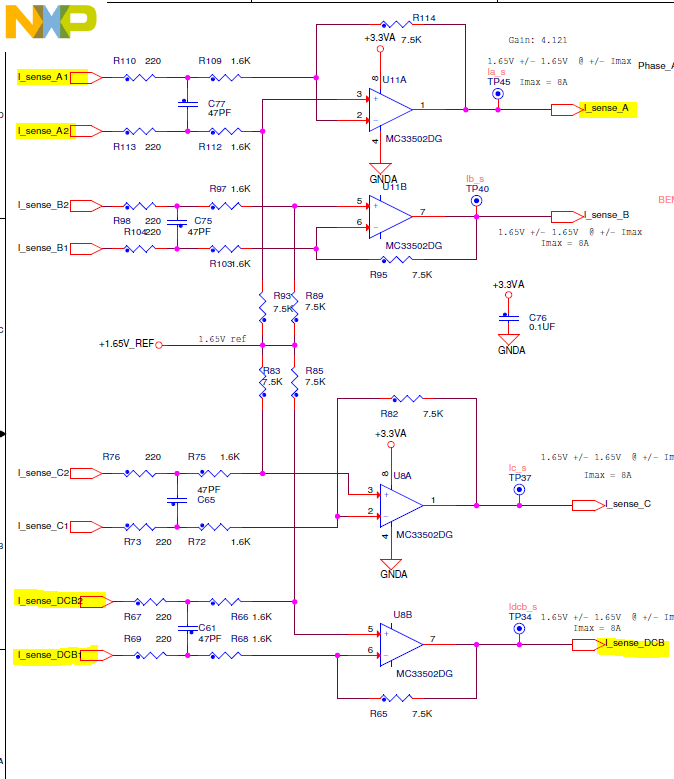
But for me it is not possible to measure any current with I_dcb shunt.
I have tried this with two HVP-MC3PH board (but with the same Controller Card)
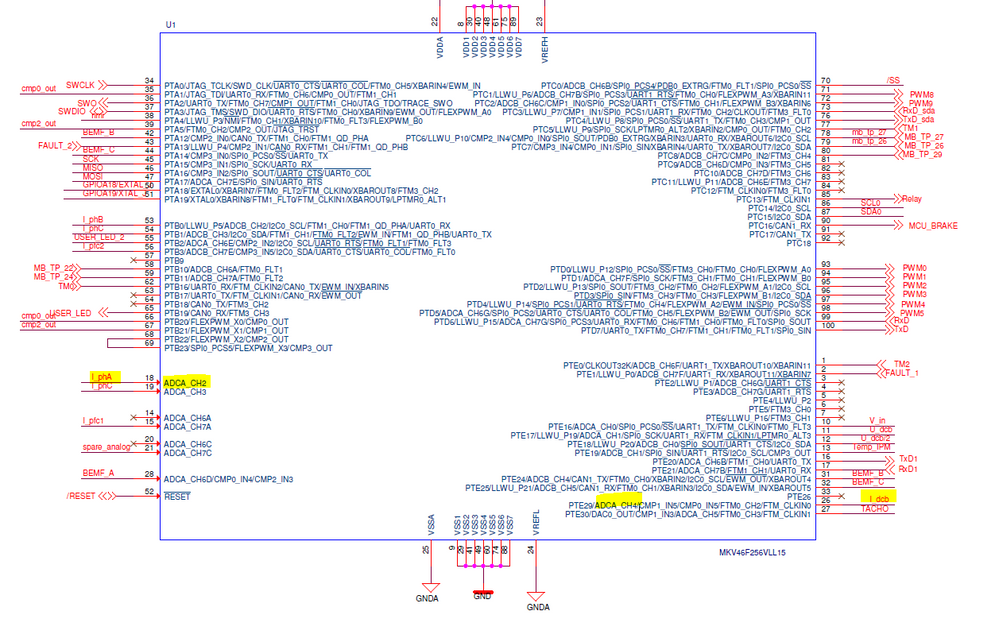
Here you can see the config of my adc samples:
I don't understand why there isn't any value for I_dcb...
Do you have an idea or did I anything wrong ?
Best regards
Leon
Hello Daniel,
now also this example works with KV4 !
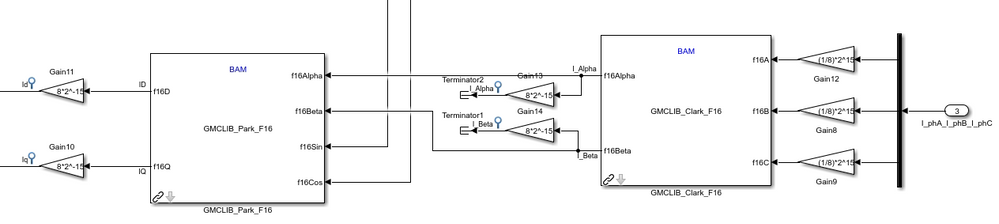
In the Fast Loop I have modified this:
The Sub block which is not in the kv4 library I have used a Standard simulink add block.
Of course with subtracting the second Input.
What I have seen in you Fig 13 and 15 is that you didn't reset the Controllers !
So the Controller Outputs are not 0 at the Moment after alignment.
They are calculating the Output directly after downloading the code from matlab.
I decided to reset the Controllers with negative edge from "ExecuteAlign".
Also you did not activate the anti wind up in the advanced Options. This would be a further optimization.
Kind regards
Leon
Leon,
Nice job! looks like i need to hurry with Sensoless module because you are catching up very fast :-)
What I have seen in you Fig 13 and 15 is that you didn't reset the Controllers !
I did it in the next module: https://community.nxp.com/thread/471093 Fig. 30 - with many other tricks to allow CW or CCW directions.
Hello Daniel,
also for the Fast Loop I have a question.
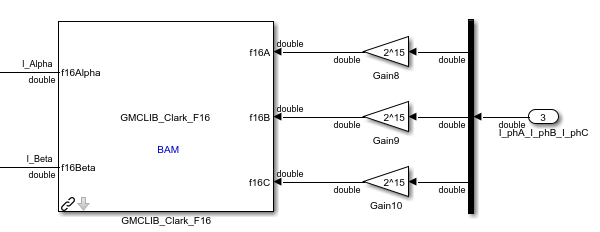
The contained blocks GMCLIB_Park_FLT and GMCLIB_Clark_FLT from s32k should be replaced with GMCLIB_Park_F16 and GMCLIB_Clark_F16 from kv4x. Of course with some gains like in module 5.
In case of U_d and U_q from module 5 it works with gain 2^15 because U_d and U_q are always between 0 and 1.
Now for scaling the currents for GMCLIB_Clark_F16 this might don't work because they are not always between 0 and 1 A ?
How to make the currents suitable for the Clark_F16 block ?
Obviously there isn't a MLIB_Sub block for kv4x (for the PI Controller) ?
How should I replace the Sub block for KV4x ?
Best regards
Leon