Position Reckoning

[chudaidai]

Hi,

I have mounted the FRDM-FXS-MULT-B and FRDM-KL25Z on a mobile platform to record it's trajectory，and I use the linear acceleration obtained from Sensor Fusion Library, but the line recorded is not similiar to the trajectory, and I don't know what caused the problem and how to solve it...

Thanks

ChuDaidai

[chudaidai]

Hi,Mike

     Thank you very much!

ChuDaidai

[michaelestanley]

My friend Mark, who is THE expert on accelerometer calibration, noted that my 2nd example above is too optimistic.  I also found an error in the above script in that it was only running for 2.5 seconds.

Mark suggested I use 350 micro-g calibrated post-board-mount offset.   Which is still optimistic for some devices, but represents something he's done in the lab.   In which case our error can extend to greater than 40cm in 5 seconds.

[scottm]

Hi Mike,

This is a purely hypothetical question and I have no intention of trying to tackle it any time soon, but if you were to incorporate two or more complete sets of sensors in a device, would you be able to reduce some of those error terms?

The SyFy series 'The Expanse' featured a 'bugged' wooden pencil that electronically recorded everything it was used to write.  It'd make for an interesting sensor fusion project for a tiny Cortex M0+ MCU and sensor package if your displacement measurement was accurate enough in the short term.  :smileywink:

I'm also curious how a priori knowledge of the mechanics and constraints of a  device like that (or like the hula hoops that are one of my major products) might be used to improve the accuracy of the sensor fusion algorithms, but I suspect the math is well beyond me.

Scott

[michaelestanley]

Assuming Gaussian noise (which I do), you're always better off with additional samples, as it will tend to average out.  As to post-board-mount offset, I do not know if that follows a Gaussian distribution (perhaps someone else can chime in if they know that answer).  But if it did, you could argue that with a sufficiently high level of redundancy, that would average out as well.

I think the "bugged" pencil you mention isn't all that far out, as you could make some simplifying assumptions about time durations and motions.   It would probably be easier for those writing text verus cursive, as you could take advantage of the change in Z to segment the data.

[michaelestanley]

ChuDaidai,

Replace the words "work well" with "work better" and it would be closer to the truth.  We are working on an addition that will allow you to calibrate out post-board mount offset of an accelerometer at 1 temperature.   BUT you still have the effects of random noise in the accelerometer output.  Integrating random noise creates something called "random walk".

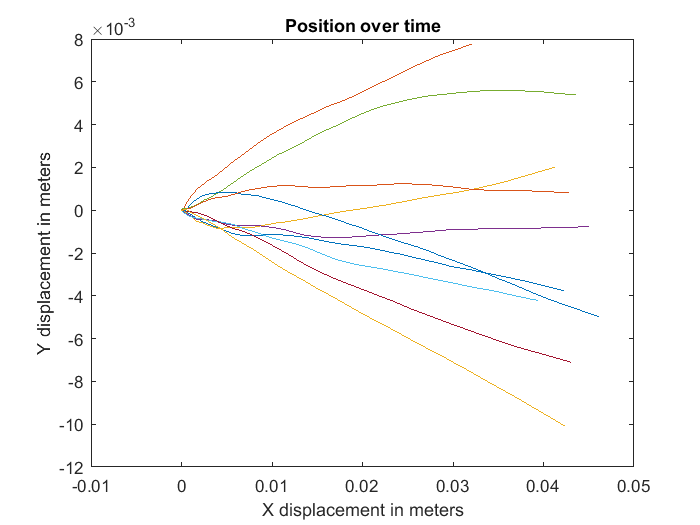
In the figure below, I took noise and post-board-mount offset numbers from the MMA8451Q datasheet.  I modelled 20mg offset all in the X axis.  Noise in both X and Y.  After 5 seconds, we have greater than 60cm error in X and about 2mm error in Y.  The X error can be cut down to approximate the Y error by calibrating the accelerometer after the PCB is populated.  There's nothing you can do about the noise terms.

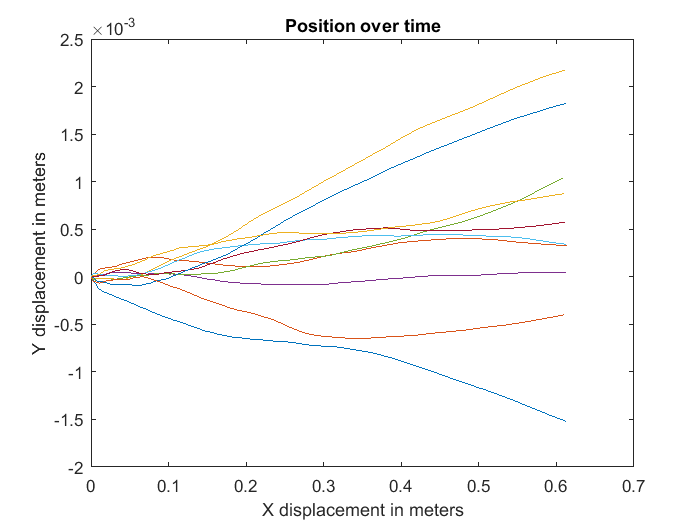
With offset reduced to 1 microG, the curve looks like:

But again, this is using a single-temperature offset correction.  Variations in temperature will cause the terms to increase.

I've included the Matlab script that computed the first graph below, so you can play with it yourself.

Mike

close all;
runs = 10;          %% Number of runs to simulate
g = 9.80665;        %% 1 g = 9.8 meters/sec/sec
N = 126e-6;         %% MMA8451Q Noise = 126 micro-g per root Hz
O = [0.02, 0]*g;    %% MMA8451Q Post-board mount offset = +/- 20mg (modeled as all in X)
fs = 400;           %% sample rate
dt = 1/fs;          %% sample interval
NS = 1000;          %% Number of samples to simulate (5 seconds here)
bw = sqrt(fs);      %% bandwidth
n  = N * g * bw;    %% Noise per sample
v  = 0;           %% velocity in meters/second
cols = 1:2;
for i=1:runs
    v(1,cols)  = [0, 0];          %% 2D velocity in meters/second
    a(1,cols)  = [0, 0];          %% 2D acceleration in meters/second/second
    p(1,cols)  = [0, 0];          %% 2D position, X & Y in meters
    for j = 1:NS
        time(j)=j*dt;
        r1 = 2*rand-1;                  %% A number between -1 and 1
        r2 = 2*rand-1;                  %% A number between -1 and 1
        a(j,cols) = [r1*n, r2*n] + O;   %% measured acceleration noise
        if (j>1)
            %% now do the double integration
            v(j,cols) = v(j-1,cols) + 0.5*dt*(a(j-1,cols)+a(j,cols));
            p(j,cols) = p(j-1,cols) + 0.5*dt*(v(j-1,cols)+v(j,cols));
        end
    end
    plot(p(:,1), p(:,2)); hold on;
    title('Position over time');
    xlabel('X displacement in meters');
    ylabel('Y displacement in meters');
   
end

[michaelestanley]

ChuDaidai,

If you are trying to do "double-integration", you should stop and look for other technologies to accomplish what you are after.  Sensor noise and offset will cause this technique to explode without bound in a very short amount of time.  We are working on an improved fusion library that will include a one-temperature accelerometer calibration, but even with that, the time to which you can apply this technique is measured in only a few seconds.  It is typically only used to "aide" other techniques by helping to smooth out curves between data points taken by other sensing methods (like GPS).

Mike

[chudaidai]

Hello,Mike

What does "other technologies" mean? Other algorithms or sensors? I use the linear acceleration botained from the following formula and can I use it directly in only a few seconds?

Thanks

ChuDaidai

[michaelestanley]

ChuDaidai,

Just to be clear, you have to integrate acceleration twice to get position displacement.  Try double integrating a typical post-board mount offset of 20 or 30 mg for a couple seconds and you will see why it's useless.

As to other sensor types, it depends on your application.  Google "position sensor" and see what looks useful.

Mike

[chudaidai]

Hi, Mike

Thanks for your response! In another discussion I have heard that you will give a solution that can work well for positioning aid applications in the next version, and will it be soon? In my application, I want to use this IMU to calculate the position for just a few seconds, and I think it's unnecessary to replace it with odometer or other sensors, is this idea wrong?

Thanks

ChuDaidai