- Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- Wireless ConnectivityWireless Connectivity
- RFID / NFCRFID / NFC
- Advanced AnalogAdvanced Analog
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
- S32M
- S32Z/E
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
- Generative AI & LLMs
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
- Cloud Lab Forums
-
- Knowledge Bases
- ARM Microcontrollers
- i.MX Processors
- Identification and Security
- Model-Based Design Toolbox (MBDT)
- QorIQ Processing Platforms
- S32 Automotive Processing Platform
- Wireless Connectivity
- CodeWarrior
- MCUXpresso Suite of Software and Tools
- MQX Software Solutions
- RFID / NFC
- Advanced Analog
-
- NXP Tech Blogs
Hello, I am a little confused about the parameter setting of GFLIB_IntegratorTR_F32 function.
From the AMMCLIB manual, I get the information shown in the figure below.
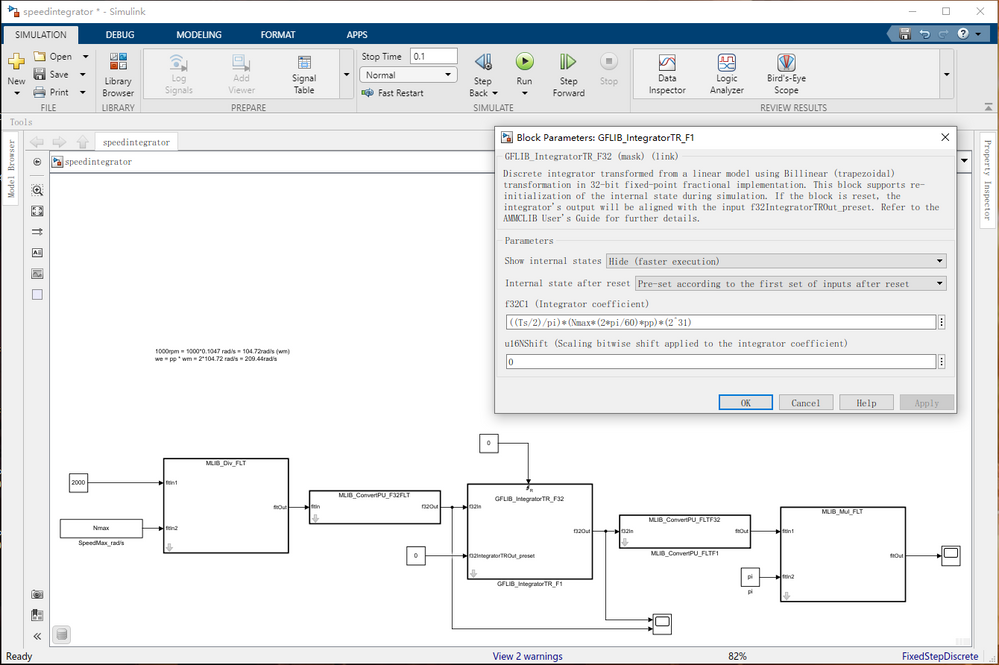
But the setting from the example shown here is different. Please see the picture below.
Support the max motor speed is Nmax, and from the AMMCLIB manual, I know that Emax is Nmax*(2*pi/60)*pp, where pp is the pole-pairs and Emax is the max electric speed of the motor. Umax is 2^31 for the f32 format.
So I think the value for the f32C1 parameter should be (Ts/2) * (Nmax*(2*pi/60)*pp) / (2^31) * 2^(-u16NShift). And the value for u16NShift parameter should be calculated according to the equation 4.
But unfortunately, I got an error using the parameter calculation method shown above.
The setting in the second figure works, namely f32C1 is equal to ((Ts/2)/pi)*(Nmax*(2*pi/60)*pp)*(2^31) and u16NShift is equal to 0. Can anyone give a detail explanation?
已解决! 转到解答。
Hello,
scaling of the physical quantities ensures that the fixed-point fractional values at the input and output of the integrator are always in the fractional range [-1; 1). The C programming language does not support fractional number format so we convert our fractional numbers to their integer equivalents (by shifting the radix point after the least significant digit). Conversion between fractional and integer number format is not scaling - it is the same set of binary digits, only the radix point changed position.
The physical quantities (speed, angle) can be expressed in whatever units you want as long as you express the scaling constant in the same units.
In your example, you expressed the desired speed in mechanical revolutions per minute (RPM) and the maximum motor speed is Nmax = 2000 RPM. You then decided to recalculate the mechanical RPM to electrical radians per second (rad/s). This implies that the rotor angle will be expressed in electrical radians. Recalculation from mechanical RPM to electrical rad/s is not scaling - we still work with physical quantities, only they are now expressed in different units.
If the input to the integrator is expressed in electrical rad/s, the input scaling constant must be also expressed in el. rad/s:
Emax = Nmax*pp*2*pi/60 = 2000*2*2*pi/60 = 418.9 el. rad/s,
where pp = 2 is the number of pole pairs.
Note that 418.9 el. rad/s is the maximum speed you can feed to the integrator - in your schematic, it looks like you are feeding in 2000 el. rad/s which is beyond the maximum and therefore an invalid value.
Assume that we want to integrate the speed which is e.g. 60 RPM. This will require two steps:
1) Recalculate RPM to el. rad/s:
N_rpm = 60 RPM
N_radps = N_rpm*pp*2*pi/60 = 60*2*2*pi/60 = 12.57 el. rad/s.
2) Scale the input to the fractional range and feed it to the integrator:
f32In = N_radps/Emax = 12.57/418.9 = 0.03, which corresponds to the Q1.31 integer 64424509.
If the integrator integrates el. rad/s, the output angle will be expressed in electrical radians, i.e. the output range is [-pi, pi). To scale this range to the fractional range, we must set the output scaling constant to:
Umax = pi
the unit is the same as the output, i.e. electrical radians.
Finally, the scaled integration coefficient is:
C1f = Ts/2*Emax/Umax = Ts/2*(Nmax*pp*2*pi/60)/pi
If the coefficient value fits in the fractional range, we can set u16NShift = 0 and the above value of C1f does not need further shifting by u16NShift. The coefficient can be converted from fractional format to the Q1.31 integer format by shifting the radix point after the least significant bit:
C1f_integer = C1f*(2^31)
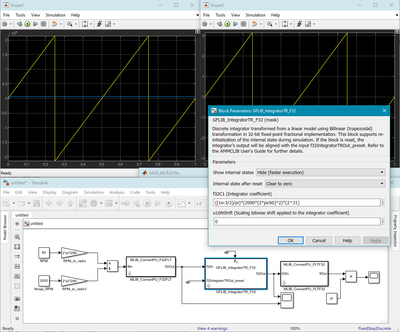
Attached is a screenshot of an example integrator with input speed of 60 RPM, Ts = 1 ms, the simulation runs for 1 second. We can see that the integrator output correctly completes two electrical revolutions.
BR,
Petr
Hello,
scaling of the physical quantities ensures that the fixed-point fractional values at the input and output of the integrator are always in the fractional range [-1; 1). The C programming language does not support fractional number format so we convert our fractional numbers to their integer equivalents (by shifting the radix point after the least significant digit). Conversion between fractional and integer number format is not scaling - it is the same set of binary digits, only the radix point changed position.
The physical quantities (speed, angle) can be expressed in whatever units you want as long as you express the scaling constant in the same units.
In your example, you expressed the desired speed in mechanical revolutions per minute (RPM) and the maximum motor speed is Nmax = 2000 RPM. You then decided to recalculate the mechanical RPM to electrical radians per second (rad/s). This implies that the rotor angle will be expressed in electrical radians. Recalculation from mechanical RPM to electrical rad/s is not scaling - we still work with physical quantities, only they are now expressed in different units.
If the input to the integrator is expressed in electrical rad/s, the input scaling constant must be also expressed in el. rad/s:
Emax = Nmax*pp*2*pi/60 = 2000*2*2*pi/60 = 418.9 el. rad/s,
where pp = 2 is the number of pole pairs.
Note that 418.9 el. rad/s is the maximum speed you can feed to the integrator - in your schematic, it looks like you are feeding in 2000 el. rad/s which is beyond the maximum and therefore an invalid value.
Assume that we want to integrate the speed which is e.g. 60 RPM. This will require two steps:
1) Recalculate RPM to el. rad/s:
N_rpm = 60 RPM
N_radps = N_rpm*pp*2*pi/60 = 60*2*2*pi/60 = 12.57 el. rad/s.
2) Scale the input to the fractional range and feed it to the integrator:
f32In = N_radps/Emax = 12.57/418.9 = 0.03, which corresponds to the Q1.31 integer 64424509.
If the integrator integrates el. rad/s, the output angle will be expressed in electrical radians, i.e. the output range is [-pi, pi). To scale this range to the fractional range, we must set the output scaling constant to:
Umax = pi
the unit is the same as the output, i.e. electrical radians.
Finally, the scaled integration coefficient is:
C1f = Ts/2*Emax/Umax = Ts/2*(Nmax*pp*2*pi/60)/pi
If the coefficient value fits in the fractional range, we can set u16NShift = 0 and the above value of C1f does not need further shifting by u16NShift. The coefficient can be converted from fractional format to the Q1.31 integer format by shifting the radix point after the least significant bit:
C1f_integer = C1f*(2^31)
Attached is a screenshot of an example integrator with input speed of 60 RPM, Ts = 1 ms, the simulation runs for 1 second. We can see that the integrator output correctly completes two electrical revolutions.
BR,
Petr
How do I set my parameters if I want to get the integration result of 65535 circles through the 32-bit integrator? Suppose my Emax = Nmax*pp*2*pi/60 = 2000*2*2*pi/60 = 418.9 el.rad /s, and my Umax = pi*65535 according to my idea. However, when I run the integrator in keil, it doesn't work. I don't quite understand the reason, looking forward to your reply, I would appreciate it!
The 32-bit integrator overflows when it reaches the maximum value. If you need to express the integrator output in 16-bit fixed-point fractional type, you can use the conversion function MLIB_ConvertPU_F16F32:
#include "mlib.h"
#include "gflib.h"
tFrac32 my_32bit_integrator_output;
tFrac16 my_16bit_converted_value;
my_32bit_integrator_output = GFLIB_IntegratorTR_F32(...);
my_16bit_converted_value = MLIB_ConvertPU_F16F32(my_32bit_integrator_output);
Alternatively, the integrator function is also available in 16-bit fixed point implementation, in which case the input and output are both 16-bit fractional values.
I am working on motor control calculations and would like to implement an integrator for electrical angle accumulation. My plan is as follows:
I will use a 16-bit integrator to integrate the electrical angle.
Additionally, I want to use a 32-bit integrator to accumulate the electrical angle over time.
The 32-bit integrator should work in such a way that when the 16-bit integrator completes a full cycle (360° and overflows from 360° back to 0°), the 32-bit integrator continues accumulating without resetting.
This setup allows me to track the accumulated electrical angle over a long period while still using a 16-bit resolution for real-time angle integration.
Could you please advise on the best approach to implement this using NXP’s motor control solutions? Specifically, I am interested in how to efficiently handle the overflow of the 16-bit integrator and properly increment the 32-bit accumulator while ensuring smooth operation in real-time motor control applications.
I would appreciate any insights or recommendations you can provide.