- Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- Wireless ConnectivityWireless Connectivity
- RFID / NFCRFID / NFC
- Advanced AnalogAdvanced Analog
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
- S32M
- S32Z/E
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
- Generative AI & LLMs
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
- Cloud Lab Forums
-
- Knowledge Bases
- ARM Microcontrollers
- i.MX Processors
- Identification and Security
- Model-Based Design Toolbox (MBDT)
- QorIQ Processing Platforms
- S32 Automotive Processing Platform
- Wireless Connectivity
- CodeWarrior
- MCUXpresso Suite of Software and Tools
- MQX Software Solutions
- RFID / NFC
- Advanced Analog
-
- NXP Tech Blogs
- Home
- :
- Model-Based Design Toolbox (MBDT)
- :
- Model-Based Design Toolbox (MBDT)
- :
- The question About the GFLIB_Asin function in NXP
The question About the GFLIB_Asin function in NXP
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
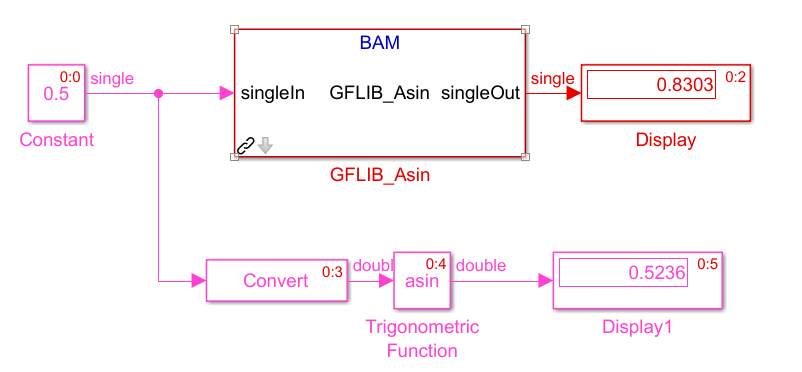
The model about the GFLIB_Asin function comparing with the Asin Math Function in Matlab/Simulink:
As above Shown,The input paramater is 0.5 ,but the answer is difference,why?who can help us ,Thanks a lot.
Solved! Go to Solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Eden Li,
With this question you have opened the Pandora's box of numerical methods on embedded system :-)
There are a lot of technical articles about numeric approximations in the field of transcendental functions. Since we are dealing with an embedded system where time matters - we need to take into account some "shortcuts" when computing a specific function. In other words, you do not want to spend a great amount of time computing a number with a high precision by introducing penalties to other critical processes.
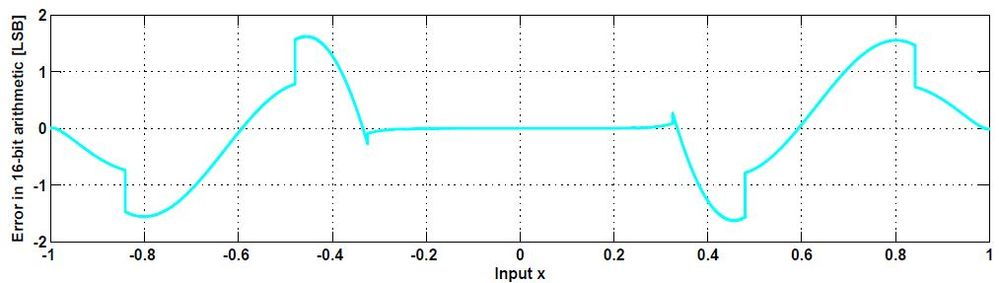
For this particular case asin(x), the implementation is using the Taylor polynomial approximation for 2 different numerical intervals: [0, 0.4) with relative good precision using a specific set of polynomial coefficients and [0.4, 1) with "some" precision using a different set.
On the other hand, the Matlab is using the FDLIBM implementation (you can get details here: http://www.netlib.org/fdlibm/e_asin.c ) which gives much better results but the execution time is longer if implemented on MPC564x e200@150MHz.
Hence, the difference results depending on the value received as input between our implementation and the one from Matlab. If we compare the 2 methods over the entire range of inputs we get:
As said before, you need to accept a trade off between speed vs. precision.
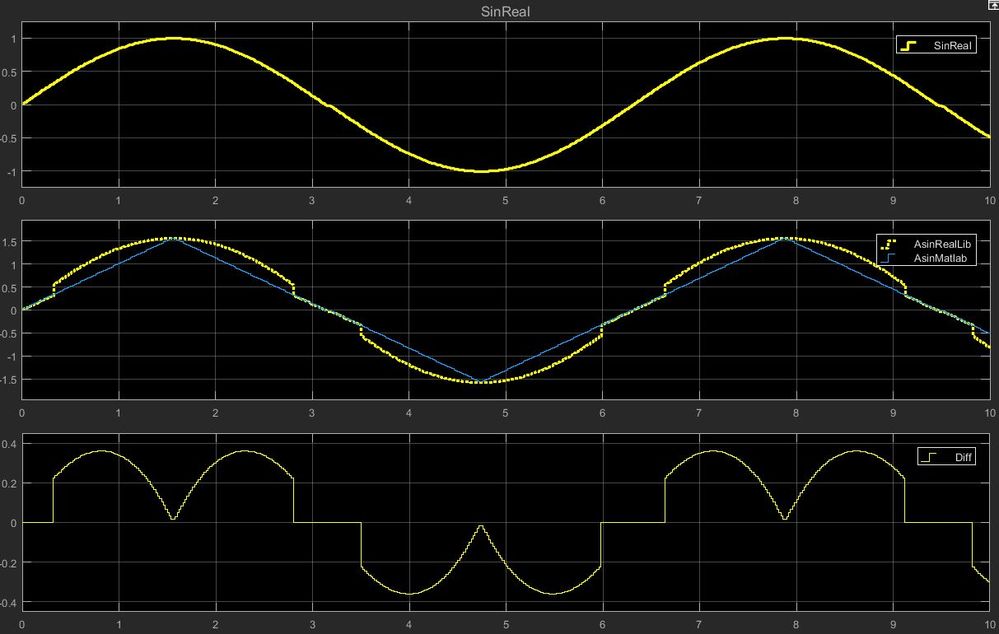
If we compare the output dynamically for an input sine signal [-1,1] we get the following:
For the reference I've included a model to replicate this.
Hope this clarify your concern!
Best regards,
Daniel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Eden Li,
With this question you have opened the Pandora's box of numerical methods on embedded system :-)
There are a lot of technical articles about numeric approximations in the field of transcendental functions. Since we are dealing with an embedded system where time matters - we need to take into account some "shortcuts" when computing a specific function. In other words, you do not want to spend a great amount of time computing a number with a high precision by introducing penalties to other critical processes.
For this particular case asin(x), the implementation is using the Taylor polynomial approximation for 2 different numerical intervals: [0, 0.4) with relative good precision using a specific set of polynomial coefficients and [0.4, 1) with "some" precision using a different set.
On the other hand, the Matlab is using the FDLIBM implementation (you can get details here: http://www.netlib.org/fdlibm/e_asin.c ) which gives much better results but the execution time is longer if implemented on MPC564x e200@150MHz.
Hence, the difference results depending on the value received as input between our implementation and the one from Matlab. If we compare the 2 methods over the entire range of inputs we get:
As said before, you need to accept a trade off between speed vs. precision.
If we compare the output dynamically for an input sine signal [-1,1] we get the following:
For the reference I've included a model to replicate this.
Hope this clarify your concern!
Best regards,
Daniel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi,Dumitru-daniel.popa,thank you very much for your reply,Iam very grateful for your help!