- Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- Wireless ConnectivityWireless Connectivity
- RFID / NFCRFID / NFC
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
- S32M
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
- Cloud Lab Forums
-
- Knowledge Bases
- ARM Microcontrollers
- i.MX Processors
- Identification and Security
- Model-Based Design Toolbox (MBDT)
- QorIQ Processing Platforms
- S32 Automotive Processing Platform
- Wireless Connectivity
- CodeWarrior
- MCUXpresso Suite of Software and Tools
- MQX Software Solutions
- RFID / NFC
-
- RSS フィードを購読する
- トピックを新着としてマーク
- トピックを既読としてマーク
- このトピックを現在のユーザーにフロートします
- ブックマーク
- 購読
- ミュート
- 印刷用ページ
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
Hello all,
I am running the sensor fusion toolbox with a KL26Z and the latest Freedom FXS-MULT2B sensor shield.
http://www.freescale.com/webapp/sps/site/prod_summary.jsp?code=FRDM-FXS-MULT2-B
While going through the demo, I noticed some strange behavior between pitch and roll. Indeed, while physically rotating the board around its X axis (the axis going from the usb connectors to the bluetooth module), the roll never goes beyond 90 degrees, even if the board is rotated well beyond 90 degrees.
Past physically rotating above 90 degrees, the value goes down. Also, the pitch value should stay close to 0, but changes a lot and seems directly proportional to the compass (yaw) value that changes a lot as well.
On the other hand, when rotating around Y axis, pitch does exactly what I expected, going above 90 degrees when the board is rotated beyond perpendicular. And roll and compass stay almost still this time, which is also expected.
So in clear :
->pitch-only rotation : ok, only pitch affected
->roll-only rotation : not ok, roll, pitch and yaw are all affected
Did someone else noticed this behavior ? I'm using the default Android coordinates system, can this be the reason ?
PS : If i'm not clear enough please let me know, I'll try to take pictures.
解決済! 解決策の投稿を見る。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
Hi Mike, Thank you for the answer, that was the information I was looking for. I was suspecting some euler angle artifact. I sort of understand the locking at +/-90 degrees, but just out of curiosity, why is the pitch and yaw changing when the roll changes ?
At some point I would like to plot pitch and roll with an airplaine-like interface (something like this, 2 top left quadrants http://api.ning.com/files/oLv7iqkOIeTb8FF3Fv-wIcV1gh7Pgr1i6scC7hZfZUbm4266Oe5wMyvABrgYRVcgZHW3z*wDIW... ). Any chance to achieve that with a somehow robust behavior or do I must keep quaternion-based math all along ?
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
Remi,
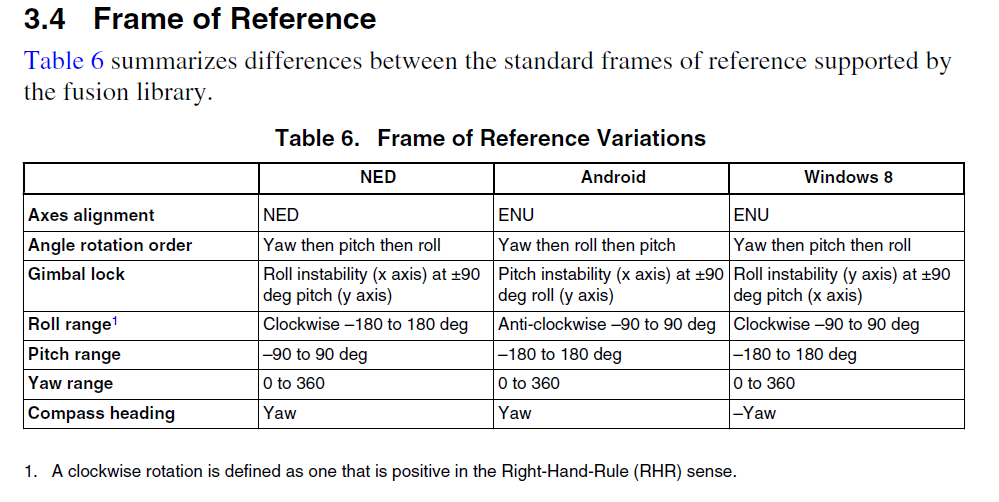
You've stumbled into the fact that things are never as simple or standardized as we would like. We've had to include options for three different frames of reference in the kit. And depending on your view, they are not always (at least to me) intuitive. They are compared in Table 6 of the sensor fusion user guide.
You can see that Roll is limited to +/- 90 degrees for Android, which correlates with your observation.
At the heart of the problem is that Euler angle representations are not unique. You can get from orientation A to orientation B via different combinations of roll, pitch and yaw. I listed 12 different variations in my blog posting at Orientation Representations: Part 1 | Embedded Beat for Design Engineers . Each one places different restrictions on the range of angles for each of roll, pitch and yaw.
From our perspective, Euler angles are useful ONLY for visualization purposes, because humans have difficulty visualizing rotation matrices and quaternions.
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
Hi Mike, Thank you for the answer, that was the information I was looking for. I was suspecting some euler angle artifact. I sort of understand the locking at +/-90 degrees, but just out of curiosity, why is the pitch and yaw changing when the roll changes ?
At some point I would like to plot pitch and roll with an airplaine-like interface (something like this, 2 top left quadrants http://api.ning.com/files/oLv7iqkOIeTb8FF3Fv-wIcV1gh7Pgr1i6scC7hZfZUbm4266Oe5wMyvABrgYRVcgZHW3z*wDIW... ). Any chance to achieve that with a somehow robust behavior or do I must keep quaternion-based math all along ?
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
It goes back to the fact that none of those numbers are really independent and is dependent upon the order in which the rotations are applied ("Angle Rotation Order" in the table).
And yes, if you are developing a graphics orientation, you should stick with quaternion-based math.
Regards,
Mike