- Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- Wireless ConnectivityWireless Connectivity
- RFID / NFCRFID / NFC
- Advanced AnalogAdvanced Analog
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
- S32M
- S32Z/E
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
- Generative AI & LLMs
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
- Cloud Lab Forums
-
- Knowledge Bases
- ARM Microcontrollers
- i.MX Processors
- Identification and Security
- Model-Based Design Toolbox (MBDT)
- QorIQ Processing Platforms
- S32 Automotive Processing Platform
- Wireless Connectivity
- CodeWarrior
- MCUXpresso Suite of Software and Tools
- MQX Software Solutions
- RFID / NFC
- Advanced Analog
-
- NXP Tech Blogs
- Home
- :
- 汎用マイクロコントローラ
- :
- LPC FAQ
- :
- How to calculate the value of crystal load capacitors?
How to calculate the value of crystal load capacitors?
- RSS フィードを購読する
- トピックを新着としてマーク
- トピックを既読としてマーク
- このトピックを現在のユーザーにフロートします
- ブックマーク
- 購読
- ミュート
- 印刷用ページ
How to calculate the value of crystal load capacitors?
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
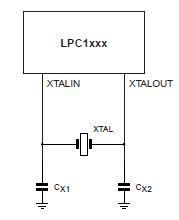
The following formula may be used to calculate a parallel resonant crystal's external load capacitors:
CL = ((CX1 x CX2) / (CX1 + CX2)) + Cstray
where:
CL = the crystal load capacitance
Cstray = the stray capacitance in the oscillator circuit, which will normally be in the 2pF to 5pF range.
Assuming that CX1=CX2 then the equation becomes:
CL = ((CX1 x CX1) / (2 x CX1)) + Cstray
CL = (CX1 / 2) + Cstray
Rearranging the equation, we can find the external load capacitor value:
CX1 = 2(CL - Cstray)
For example, if the crystal load capacitance is 15pF, and assuming Cstray=2pF, then:
CX1 = CX2 = 2(15pF - 2pF) = 26pF
It is difficult to know exactly what the stray capacitance is, but if you find the oscillation frequency is too high, the load capacitor values can be increased. If the frequency is too low, the load capacitors can be decreased.
The device data sheet may also define a maximum crystal series resistance Rs.
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
#2Submitted by larsen on Thu, 2014-11-06 03:39.
atmel defines the stray capacity as being from xtal terminal to gnd.
NXP defines the stray capacity as parallel to the crystal. This gives
Stray capacities: Catmel =2 Cnxp
so it is all a matter of definition. Anyway there are typically some "handwaving" involved in stray estimates anyway.
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
#1Submitted by ericll75 on Fri, 2014-03-28 12:38. According Atmel AVR042, p.12, the equation for the external capacitors is C = 2CL - Cstray. The same thing is reflected in Atmel AT91 ARM Thumb app note (1740A), p.7. Why the difference in equations? Why does Atmel put the stray capacitance value into CX1 or CX2 (according to AVR042, CX1 = C + Cstray), whereas the equation here puts Cstray as a separate term? Am I missing something? |