DC-DC converter DCM analysis
Most of time the DC-DC converter works on CCM, we also get lot of benefit from CCM high efficiency/low noise etc, usually we neglect the DCM status, in DCM we can get larger rippler/noise and low efficiency. Here we will give analysis.
BUCK converter
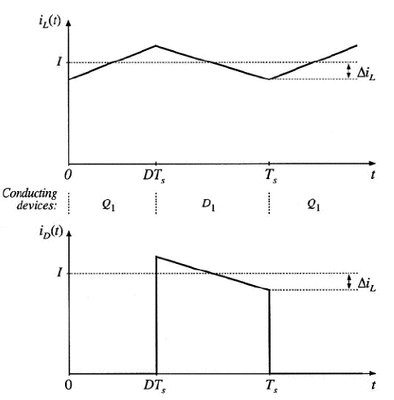
Figure2:BUCK converter in CCM inductor current iL(t),diode current iD(t)
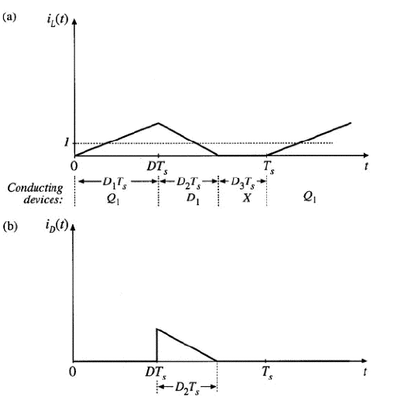
Figure2:BUCK converter in DCM inductor current iL(t),diode current iD(t)
I>△iL in CCM ; I<△iL in DCM-----(1.3)
Where I and △iL are found assuming that the converter operates in the continuous conduction mode,we put(1.1) and (1.2) into(1.3) for get in DCM.
I=V/R------(1.1)
△iL=
=
--------(1.2)
<
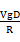
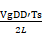
Lead to
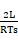
<D’
Which can be showed:
K<Kcrit(D) for DCM
Where K=2L/(RTs) and Kcrit(D)=D’
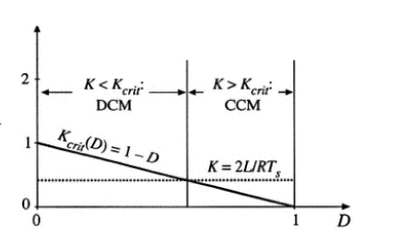
Figure3: Buck converter Kcrit(D) vs D,converter works in CCM when K>Kcrit and in DCM when K<Kcrit
Large value of K lead to CCM,small value lead to DCM for some values of duty cycle. The critical value of K at the boundary between modes,Kcrit(D) is function of duty cycle and equal with D’ for the BUCK.
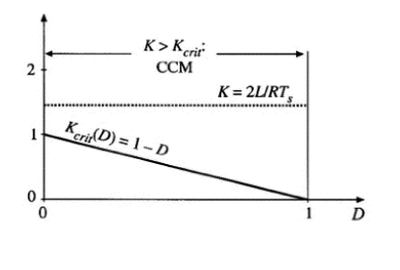
Figure4 Comparison of K with Kcrit(D),for a larger value of K. Since K>1,the converter operates in CCM for all D.
Figure4 shows work condition on the heavier loading,the R is reduced in value,such that K is larger,if K is greater than one ,then the converter operates in CCM for all duty cycle.
It is natural to express the mode boundary in terms of R,rather than the dimensionless parameter K, Equation(5.6)can be rearranged to directly expose the dependence of the mode boundary on the load resistance:
R<Rcrit(D) for CCM,R>Rcrit(D) for DCM where Rcrit(D)=2L/(D’Ts)
The converter enters DCM when R above the Rcrit.this critical value depends on the inductance,the switching period,and duty cycle.
Note that.since D’<=1,the minimum value of Rcrit is 2L/Ts.
Therefore,if R<2L/Ts,then the converter will operate in CCM for all duty cycle.
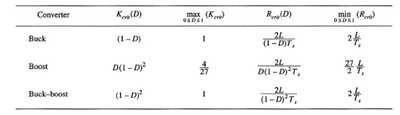
Figure5 CCM-DCM mode boundaries for the buck.boost and the buck-boost converters
The results are listed in Figure5 for three basic dc-dc converters.
In each case,the dimensionless parameters K is defined as K=2L/(RTs),and mode boundary is give by
K>Kcrit(D) or R<Rcrit(D) for CCM
K<Kcrit(D) or R>Rcrit(D) for DCM
