- NXP Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- Wireless Connectivity
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- Vigiles
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
- Cloud Lab Forums
-
- Home
- :
- Product Forums
- :
- MPC5xxx
- :
- How to set the ADC sample rate of MPC5744P?
How to set the ADC sample rate of MPC5744P?
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to set the ADC sample rate of MPC5744P?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi
Our project is VCU design, and we use MPC5744P as CPU. When designing the drivers of ADCs, we found it's hard to control the sample rate.
In the MPC5744P's reference manual, it is said that ADC's highest sample rate is 1M at 80MHz. But there's no detailed description about how to config the registers to set sample rate to the value exactly what we wanted.
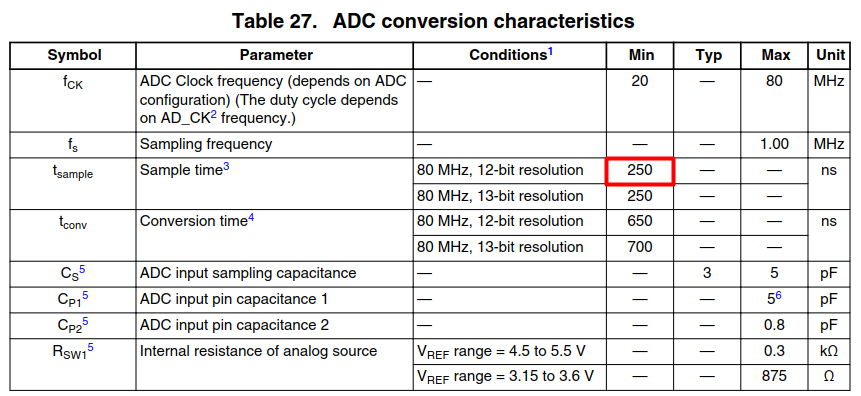
We found some description about conversion time in the 36.5.11 of reference manual, which says the total conversion time is decided by the value of ADC_MCR[ADCLKSEL], CALBISTREG[OPMODE], CTRx[INPSAMP]. But it's confusion about the relationship between the conversion time and simple rate.
As the reference manual says, the smallest value of CTRx[INPSAMP] is 8, that is to say, when CTRx[INPSAMP]=8d, the sample rate of ADC should be 1M. But if the configuration is ADC_MCR[ADCLKSEL]=1, CALBISTREG[OPMODE]=001b, CTRx[INPSAMP]=8d, the single conversion time should be 2+8+((12+1)*4)+2=64 cycles of AD_clk, and the continuous conversion time shoude be 8+((12+1)*4)+2=62 cycles of AD_clk. So in the configuration above, the sample rate in single conversion mode and continuous conversion mode are 80/66M and 80/62M, which are larger than the highest sample rate announced.
Why?
If the relationship between the conversion time and simple rate is not Simple Rate= Frequency of ADC_CLK/Conversion time, what is the true relationship?
We did some experiments, set ADC_MCR[ADCLKSEL]=1, CALBISTREG[OPMODE]=001b, CTRx[INPSAMP]=8d, and used a signal generator to generate a 1KHz triangular wave to the ADC channel, and let the MPC5744P sampled 1000 samples from the signal, then used MATLLAB simulated the waveform, but found there were about 6 periods of triangular wave, so the sample rate calculated is 80MHz/(6*1000)=133KHz. That don't make sense.
So the question is: how to set the ADC sample rate as we wanted?
Looking forward for your response!
Thanks a lot!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I'll be due to minimal sample time give by datasheet that is 250*80MHz = 20 cycles
single conversion time = 2 + 20 + ((12 + 1) x 4) + 2 = 76 cycles what's still a bit faster
It seems the overview you have highlighted on the very top describes high accuracy mode
2 + 20 + ((13 + 1) × 4) + 2 = 80 cycles
i.e. 1 MSample/sec
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for your answer!
If it's truly as you said, the ST(Sample Time) must be larger than 20 cycles, then what's the point to declare the minimum acceptable value of INPSAMP is 8 ?
davidtosenovjan, I just want to konw how to control the ADC simple rate as I wanted.Is there any equations that samply tell the working principle?
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
These are 2 different things:
- a lowest values INPSAMP that is possible to set-up (8). In this case conversion may be less accurate than specified by datasheet. For some application is may be OK, if fast conversion is the main criterion.
- a lowest values of INPSAMP that is required to choose to have set up in accordance to ADC datasheet specification to achieve specified accuracy