- NXP Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- Wireless Connectivity
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- Vigiles
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
- Cloud Lab Forums
-
- Home
- :
- Product Forums
- :
- Other NXP Products
- :
- Strange coefficient with a RBJ bandpass filtrer.
Strange coefficient with a RBJ bandpass filtrer.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Strange coefficient with a RBJ bandpass filtrer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello !
I'm trying to make a bandpass filter (constant 0dB peak gain) with the Robert Birstow-Johnson cookbook formulae. So I calculated all coefficients to fixe the bandpass filter but I have a problem with a1 coefficient value. Indeed, a1 = -1,9829.
The features of the Bandpass are :
Center frequency : fo = 1kHz
Bandwith : Bw = 1kHz => so octave Bw = 1,38. (Q = 1)
Low corner frequency : 500Hz
Hight corner frequency: 1,5kHz
Sample Frequency : Fe = 48kHz
Here is the step I did to find a1 :
w0 = 2*pi*fo/Fe = 0,13089 rad/s
S = sinw0 = 0,130526
a1 = -2*cosw0 = -1,9829 ???!! :smileyconfused:
I read the DSP56k family manual and it write : "... In the DSP56K chip family, the extreme values that a word operand can assume are - 1 and + 0.9999998. ... " .
So did I make a mistake with the calculated ?
If no, how can I implement a1 into the code ?
note : I use the dsp56374
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I searched about oscillation problem and a lot of documents around internet said it come from an overlfow problem and it's possible to resolve it by arithmetic saturation algorithme. But I can't seem to find any concrete answer about it.
Someone can help me pleas ? This is for a school project and I don't want fail
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Maxime,
Maxime Dolberg wrote:
. . . but I have a problem with a1 coefficient value. Indeed, a1 = -1,9829.
I hate it when that happens !
You have probably calculated your coefficients correctly (I did not check), it is something that happens sometimes. I have addresses it a couple of different ways.
The most brute-force way that I have used would be to substitute "-0,9829" instead of"-1,9829" in the coefficient table, and then add the "1" in as a special case after the loop completes be simply adding in the appropriate parameter. Or it could be added in before the loop starts, by replacing the clear of the accumulator with a load of the parameter into the accumulator. The advantage is that it will typically only take one extra cycle or even no extra cycles if replacing the clear. The disadvantage is that the filter code cannot be reused for other filters, as that "1" will be hard-coded in.
A more elegant way is to divide all coefficients by 2. That way, the -1,9829 would become -0.99145, and would work within the limitations of the ALU. At the end of the loop, you would then correct for the divide-by-2 by performing a left-shift on the final result. The code would then work with other filters, as long as they also had their parameters divided by 2.
There are other solutions as well, but they get more complicated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
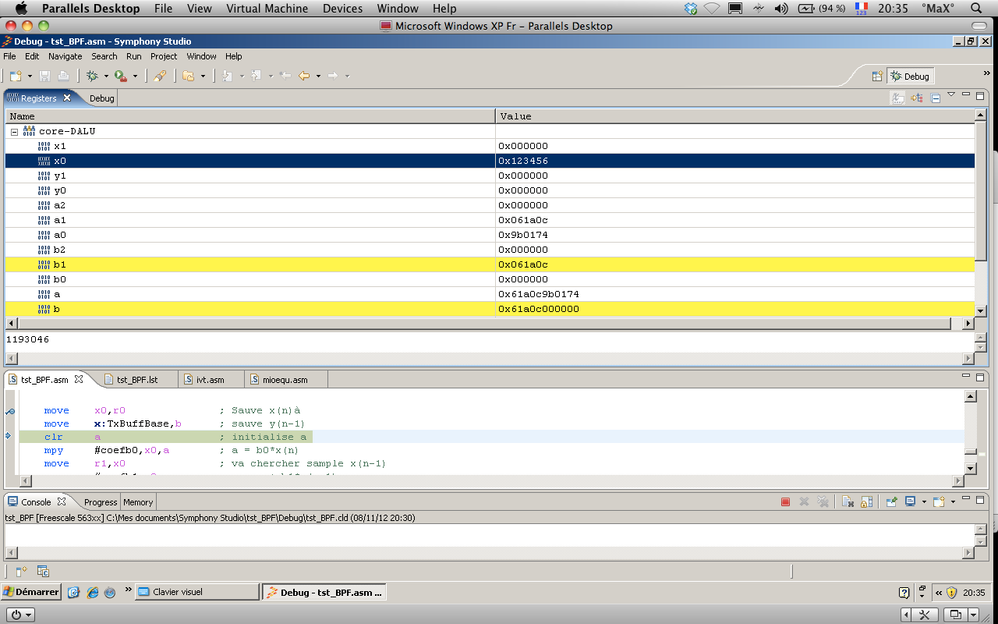
Thank you Mark for your answer, your knowledge is very helpful to me again. But by resolving this problem, I have got another one ... I sent the code in the DSP and the output result was a sinus wave oscillation with a 24kHz frequency. I think there is a link with the 48 kHz sample frequency. I'm not sure. Why is do that ?
Another thing, I have seen that the output register before the DAC truncated fractional numbers. To make it simple, I did a screen capture. 'a' is result of the last final calculation of the output (so Y(n)) and 'b' is the previous output (Y(n-1)). If you look values of this registers, 'a' is not totally equal 'b' . What going on ? I don't understand :smileyconfused: