- NXP Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- Wireless Connectivity
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- Vigiles
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
-
- Home
- :
- Identification and Security
- :
- NFC
- :
- PN532 Antenna Design question
PN532 Antenna Design question
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dear NFC community members,
I am working on designing a small RFID reader circuit that is based on the PN532 chip and I would like to get some feedback. My background isn't RF engineering, so I am not sure about many things.
I'll summarize the main questions first, and then describe in details what I've done:
I am using miniVNA Tiny for taking measurements.
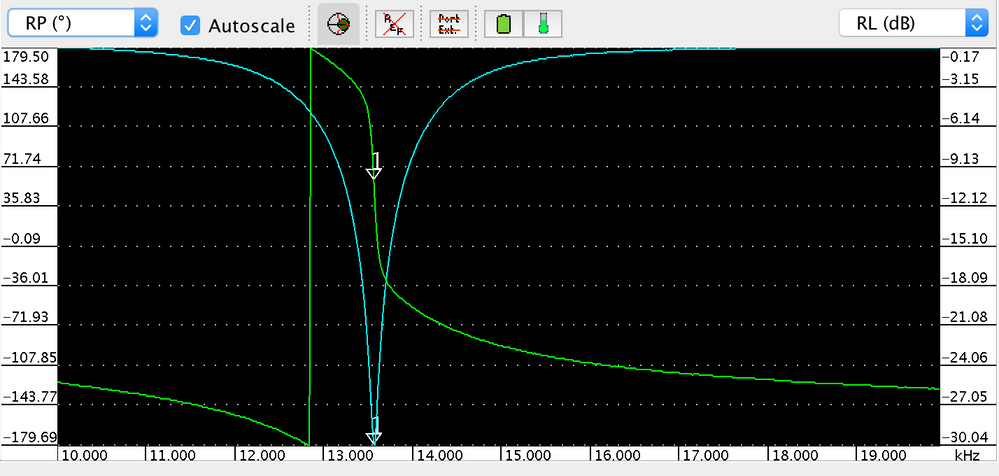
Q1: which parameter (SWR, RP, RL) should I look at for figuring out the self resonance of a circuit?
Sometimes the sign flip of RP correlates well with the minimum of RL and SWR, but not always.
Q2: Why after tuning my antenna to 13.56 Mhz (based on SWR or RL measurements) do I see a huge shift in resonance frequency when I bring a tag close to the antenna? Typically, two peaks appear: one at ~12.8Mhz and one at ~14.3Mhz? Is this normal?
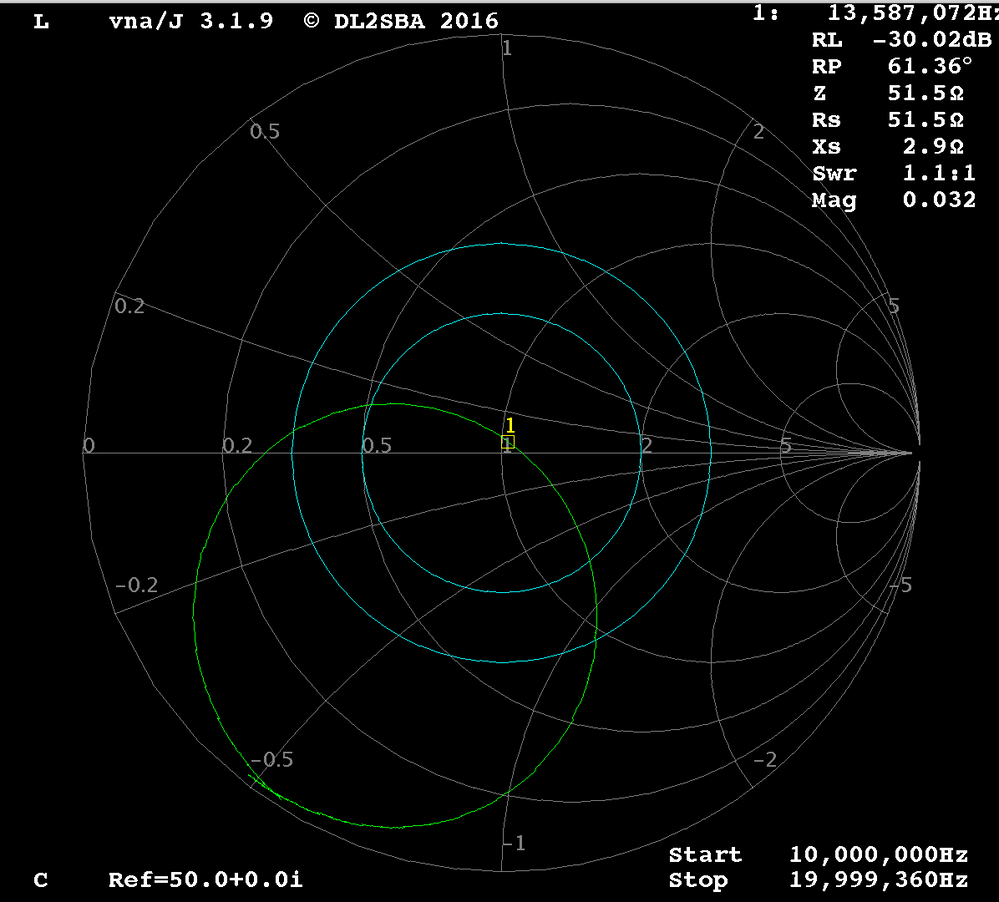
Before:
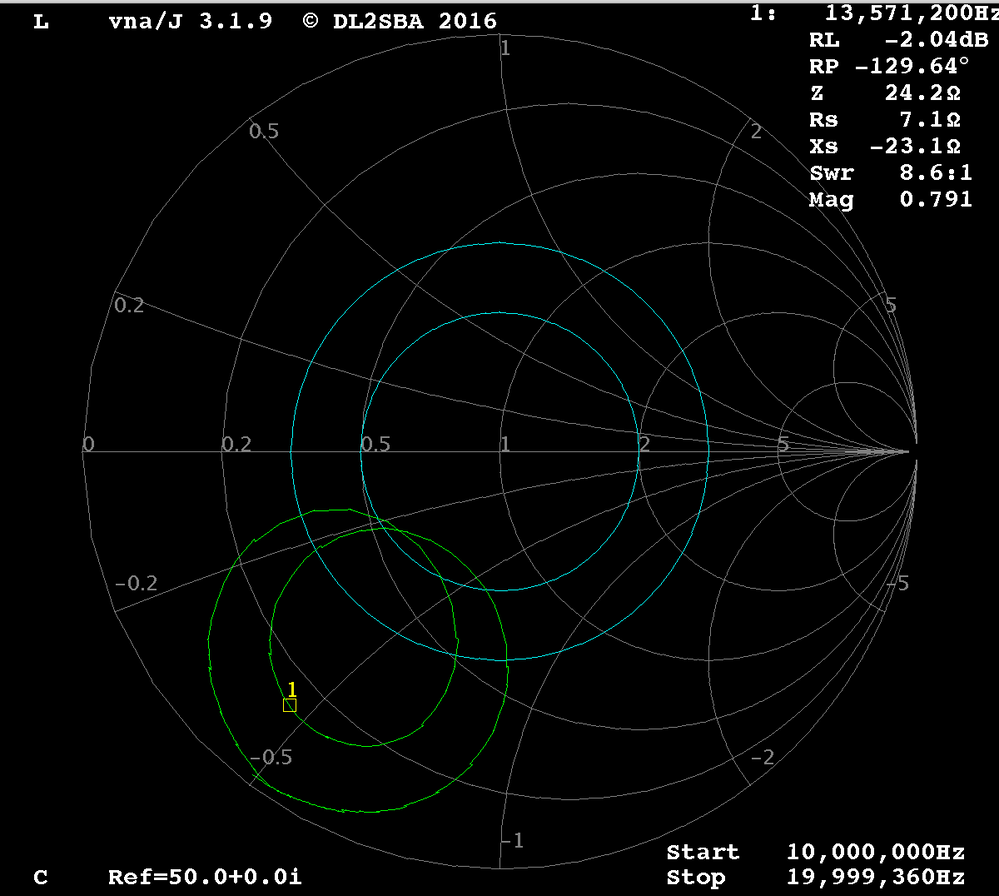
After a tag is nearby:
Full story below (and more questions below):
I basically followed the reference design and white papers describing how to tune the antenna.
The circuit has the EMC module (560nH, 220pF), series caps (C1) and parallel caps (C2).
At first, I tried to follow the general guidelines which were:
1. Measure antenna inductance (La)
I did this by measuring the reactance at 1Mhz. La = Xs / w0 = 1.6uH
This seems reasonable.
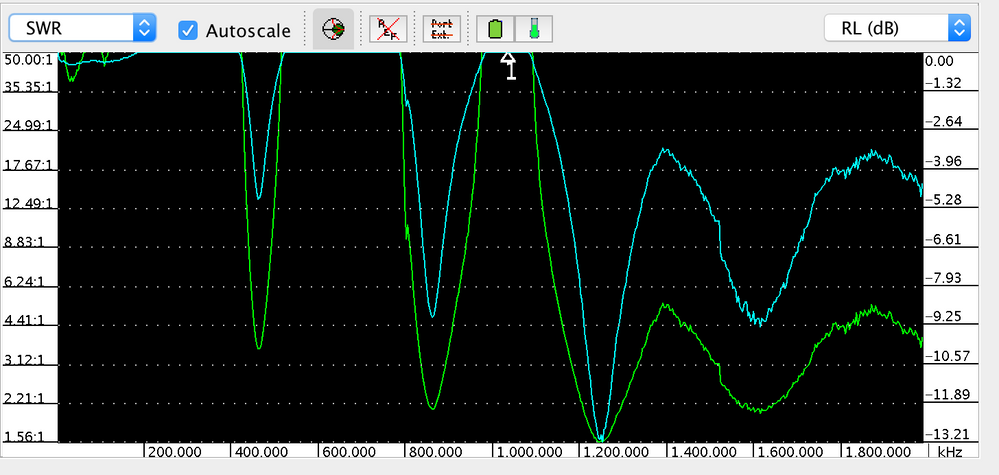
2. Measure antenna self resonance.
I looked either at the sign flip of RP or SWR.
I noticed multiple peaks, which one should I consider to be the resonance?
3. From the self resonance, estimate the antenna capacitance:
f0=1e6; % measured at 1 Mhz
w0 = 2*pi*f0;
La = Xs/w0;
Fself = 472270937;
Ca = 1/((2*pi*Fself)^2 * La);
4. Calculate C1 and C2.
I followed equations from white paper:
Ra =7.7; % Measured at 1 Mhz
Xs = 9.8; % Measured at 1 Mhz
nfc_freq = 13.56*1e6;
w = 2*pi*nfc_freq;
Qa = w*La/Ra
Rmatch = 30;
Rq = max(0, 0.5 * (w*La / Rmatch - Ra))
% in my case, no series resistors were needed. Q was ~17
% EMC filter:
L0 = 560 * 10^-9; % 560 nH
Femc_cutoff =14338865.060467; % 14.4 Mhz
C0 = (1/(Femc_cutoff*2*pi)).^2/Lemc; % 220 pF
% Calculate the series equivalent
Xtr = 2*w * ( L0 * (1-w^2*L0*C0) - Rmatch^2/4 * C0) / ((1-w^2*L0*C0)^2 + (w*Rmatch/2*C0)^2);
Rtr = Rmatch / ( (1-w^2*L0*C0)^2 + (w*Rmatch/2*C0)^2);
% Calculate the parallel equivalent circuit:
Lpa = La;
Cpa = Ca;
Rpa = (w*La)^2 / (Ra + 2*Rq);
C1 = 1/( w* (sqrt(Rtr*Rpa/4) + Xtr/2));
C2 = 1/(w^2 * Lpa/2) - 1/(w * sqrt(Rtr*Rpa/4)) - 2*Cpa;
------
The final result was:
For C1 (26.33), use 4.70 + 22.00 (=26.70), error = 0.370680 pF
For C2 (149.62), use 0.00 + 150.00 (=150.00), error = 0.380073 pF
I tried out these values, but the end result was really out of range.
Did I miss something out in my calculations?
I then played around by changing caps (without the EMC bandpass filter).
I noticed two major trends:
1. When I increase C1, I get a narrower profile (smaller arc on Smith Chart)
2. Increasing C2 generally doesn't change the radius of the arc much, but shifts the resonance frequency downward.
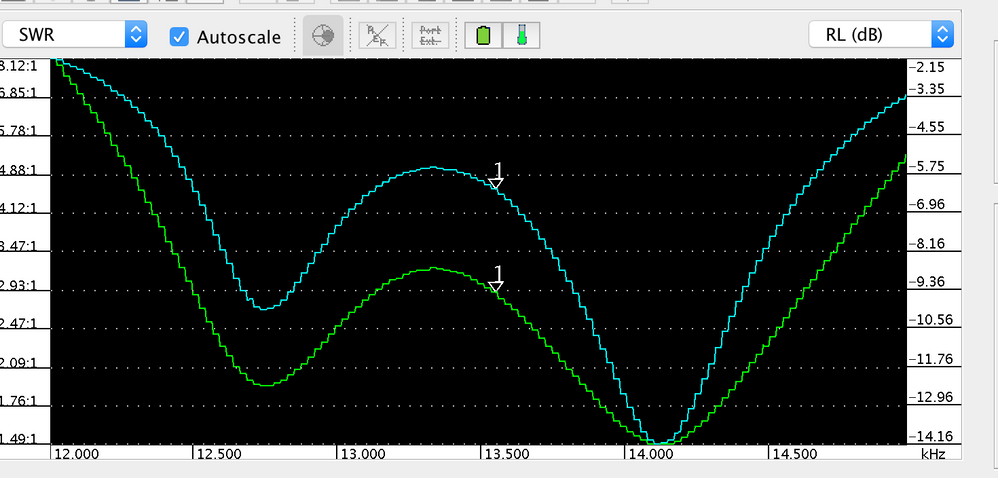
I ended up with this:
Does this look reasonable? If so, why do I get such a huge detuning when a tag is near by?
Solved! Go to Solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
OK. I followed the steps laid out in AN1445. That is the most useful document on the issue.
The flow chart for tuning C1 and C2 really helped.
Now the antenna is properly tuned and the circuit works!
A critical step is setting the correct resistance on the receiver voltage divider circuit. I fried my first board because the returned voltage exceeded 1V :smileyhappy:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello shayohayon,
I will order mini Vna tiny to tune my Antenna, as you mentioned you used it in your design.
Is it working without problems? because NXP recommends to use only mini VNA PRO.
Thank you
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
OK. I followed the steps laid out in AN1445. That is the most useful document on the issue.
The flow chart for tuning C1 and C2 really helped.
Now the antenna is properly tuned and the circuit works!
A critical step is setting the correct resistance on the receiver voltage divider circuit. I fried my first board because the returned voltage exceeded 1V :smileyhappy:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello Shay,
I asked for help of NFC expert team on your questions, the following is answers!
----------------------------
Q1: which parameter (SWR, RP, RL) should I look at for figuring out the self resonance of a circuit?
Sometimes the sign flip of RP correlates well with the minimum of RL and SWR, but not always.
[Answer] We just check Rs value for matching when Xs is close to 0 @13.56MHz.
Q2: Why after tuning my antenna to 13.56 Mhz (based on SWR or RL measurements) do I see a huge shift in resonance frequency when I bring a tag close to the antenna? Typically, two peaks appear: one at ~12.8Mhz and one at ~14.3Mhz? Is this normal?
[Answer] It is normal when a tag/card or other metal circuit close to the antenna. The coupling effect will detune the original matching.
More antenna matching guide can be found on the following link:
------------------------------
Regards,
Weidong
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Bump? Any takers? Has anyone designed a custom antenna and went through this process before?