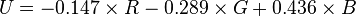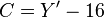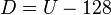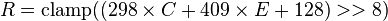- NXP Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- Wireless Connectivity
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- Vigiles
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
-
- Home
- :
- i.MX Forums
- :
- i.MX Processors
- :
- YUV422->RGB24 - which conversion formula does IPU use?
YUV422->RGB24 - which conversion formula does IPU use?
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
YUV422->RGB24 - which conversion formula does IPU use?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
I created a 800x600 RGB24 buffer filled with 0x80 i.e; (R, G, B) = (128, 128, 128) or 0x808080 . I then use IPU to convert RGB24->YUV422 (see below for the code snippet). As expected the resultant buffer has YUV= 0x808080.
Converting back to RGB24, however, has unexpected result. The resulting RGB buffer has (R, G, B) = (130, 128, 127) or 0x82807F.
Which conversion does IPU apply?
Based on Wikipedia's YUV page, RGB should either be 0x808080 (ITU-R version) or 0x828282 (if IPU assumes YCbCr format for YUV->RGB conversion).
Any input is greatly appreciated.
Thanks!
YUV - Wikipedia, the free encyclopedia
Excerpt from Wikipedia:
These formulae are based on the NTSC standard;
On older, non-SIMD architectures, floating point arithmetic is much slower than using fixed-point arithmetic, so an alternative formulation is:
Using the previous coefficients and noting that clamp() denotes clamping a value to the range of 0 to 255, the following formulae provide the conversion from Y'UV to RGB (NTSC version):
Note: The above formulae are actually implied for YCbCr. Though the term YUV is used here, it should be noted that YUV and YCbCr are not exactly the same in a strict manner.
The ITU-R version of the formulae is different:
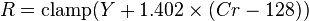
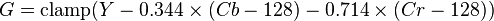
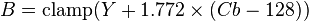
- Code snippet:
// set task basics
memset( &ipuTask, 0, sizeof(ipuTask) );
ipuTask.input.width = inW;
ipuTask.input.height = inH;
ipuTask.input.format = inFmt;
ipuTask.output.width = outW;
ipuTask.output.height = outH;
ipuTask.output.format = outFmt;
// get image file and check for failure
// compute input size in bytes
iInputSize = ipuTask.input.width * ipuTask.input.height *
computeBPP( ipuTask.input.format ) / 8;
// set the amount of memory needed for the task input
ipuTask.input.paddr = iInputSize;
// allocate memory for the input image and check for failure
// (NOTE: input.paddr will be replaced with the physical address)
iRetValue = ioctl( iIPUFD, IPU_ALLOC, &ipuTask.input.paddr );
if( iRetValue < 0 )
{
perror( "ioctl(IPU_ALLOC)" );
Cleanup();
return iRetValue;
}
// map virtual address to input memory
pInputBuff = mmap( 0, iInputSize, PROT_READ | PROT_WRITE,
MAP_SHARED, iIPUFD, ipuTask.input.paddr );
if( !pInputBuff || pInputBuff == MAP_FAILED )
{
perror( "mmap" );
Cleanup();
return -1;
}
// compute output size in bytes
iOutputSize = ipuTask.output.width * ipuTask.output.height *
computeBPP( ipuTask.output.format ) / 8;
// set the amount of memory needed for the task output
ipuTask.output.paddr = iOutputSize;
// allocate memory for the output image and check for failure
// (NOTE: output.paddr will be replaced with the physical address)
iRetValue = ioctl( iIPUFD, IPU_ALLOC, &ipuTask.output.paddr );
if( iRetValue < 0 )
{
perror( "ioctl(IPU_ALLOC)" );
Cleanup();
return iRetValue;
}
// map virtual address to output memory
pOutputBuff = mmap( 0, iOutputSize, PROT_READ | PROT_WRITE,
MAP_SHARED, iIPUFD, ipuTask.output.paddr );
if( !pOutputBuff || pOutputBuff == MAP_FAILED )
{
perror( "mmap" );
Cleanup();
return -1;
}
// get output file and check for failure
fOutput = fopen( outName.c_str(), "wb" );
if( fOutput < 0 )
{
cerr << "failed to open " << outName.c_str() << endl;
Cleanup();
return -1;
}
// read input image
iRetValue = fread( pInputBuff, 1, iInputSize, fInput );
if( iRetValue < iInputSize )
{
perror( "fread" );
Cleanup();
return -1;
}
// execute the IPU task and check for failure
iRetValue = ioctl( iIPUFD, IPU_QUEUE_TASK, &ipuTask );
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Please refer to section 37.4.5.4 (Main Processing Section), item 4 of the i.MX6 DQ Reference
Manual.
http://cache.freescale.com/files/32bit/doc/ref_manual/IMX6DQRM.pdf
"4. First color space conversion YUV to RGB or RGB to YUV with the conversion
matrix CSC1. The conversion matrix coefficients are programmable. They are stored
in the Task Parameter Memory."
Have a great day,
Yuri
-----------------------------------------------------------------------------------------------------------------------
Note: If this post answers your question, please click the Correct Answer button. Thank you!
-----------------------------------------------------------------------------------------------------------------------