- NXP Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- Wireless Connectivity
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- Vigiles
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
- Cloud Lab Forums
-
- Home
- :
- Model-Based Design Toolbox (MBDT)
- :
- Model-Based Design Toolbox (MBDT)
- :
- Normalized Floating Point Numbers and why we used them in MBD Toolbox
Normalized Floating Point Numbers and why we used them in MBD Toolbox
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Normalized Floating Point Numbers and why we used them in MBD Toolbox
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Just recently I've received an email with a few questions regarding one particular block (GMCLIB_SvmStd_FLT) from the MPC5744 MBD Toolbox exposed by the AMMCLIB, and I thought it would be nice to share the knowledge here since other might face similar questions.
So, here is the background (I've remove sensitive personal information from the email):
..., the SVM_STD_FLT block can accept whatever input value in the range of the floating 32 bits and then scale it internally to either [0,1] or [-1,1].!
But, from what I can see in my simulations, the Output of the SVM is not saturated only if the input to is a [-1,1] sin/cos inputs. Which means that the SVM_STD_FLT does not really accept floating inputs..! Do I need to normalize the inputs to [-1,1] even for a floating input SVM?
Regarding the output of the SVM, should it be exactly changing from 0 to 1 in order to have proper operation of the power stage ? or it could be changing between any [min, max] values inside [0,1]!
As you can see there a few a good points here, therefore let us discuss upon those. It is not in my intention to provide a deep lecture on floating point but I just want to point out a few things to clarify the subject.
Let us start with the most obvious one:
Do I need to normalize the inputs to [-1,1] even for a floating ...?
In my opinion, we should always do that when working with embedded systems and it has to do with precision.
Let me explain why:
Any real number can be represented in binary form as:
I(m) I(m-1) ... I(2) I(1) I(0) . F(1) F(2) ... F(n-1) F(n)
where: I(k) and F(k) is 0 or 1 of the Integer or Fraction parts respectively
The IEEE 754 binary representation defines the floating point on 32bit as single precision using this format:
(-1)^s x c x 2^e
where: s = sign (0 or 1), c = significant coefficient/mantissa and e = exponent
In case of single precision representation on 32bit microprocessors we will have:
- 1 bit for sign
- 8 bits for exponent
- 23 bits for significant/mantissa
Let's take as an example the following fraction:
9/2(b10) = 4.5(b10) = 100.1(b2)
By definition the result said to be normalized if it is represented with leading 1 bit:
100.1(b2) -> normalized -> 1.001(b2) x 2^2
Since all hardware implementations are using the boolean algebra (...because transistors :-) ) and since normalized numbers means the left most bit it must be 1 - then the logic question is: If it is always 1 then why should we actually store it ?
Many floating point representations have this implicit hidden bit in the mantissa. This is a bit which is present virtually in the mantissa, but not stored in memory because its value is always 1 in a normalized number. This rule allows the memory format to have one more bit of precision.
The mantissa of a floating point number represents an implicit fraction whose denominator is the base raised to the power of the precision. Since the largest representable mantissa is one less than this denominator(base raised to the power of the precision), the value of the fraction is always strictly less than 1. More bits in the mantissa = better precision of floating point numbers
Regarding the second aspect:
Output of the SVM is not saturated only if the input to is a [-1,1] sin/cos inputs
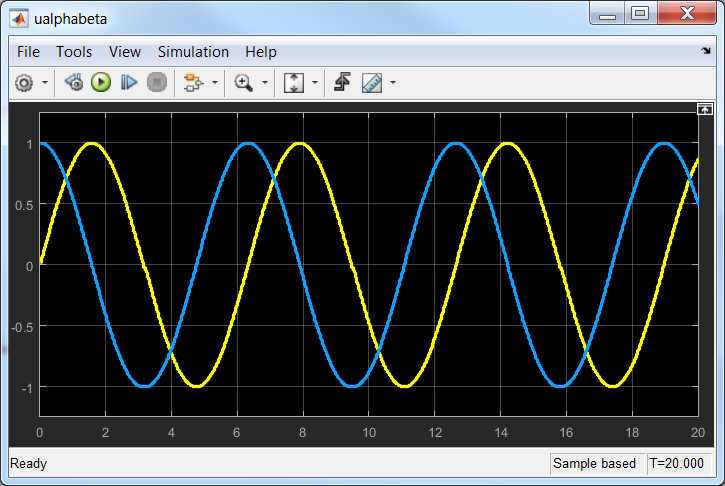
The inputs to the Space Vector Modulation block represents the 3-phase stator voltages Ua, Ub, Uc that are transformed via the Inverse Clarke Transformation into Ualpha, Ubeta 2-phase orthogonal coordinate system.
In general in embedded system - and in particular in motor control application - all the variables are scaled relatively to maximum values supported by the system sensors. In case of voltages, the shunts/opams/adc chains are design to support a maximum read out. Therefore all the quantities derived or that relates with the voltage are scaled to the [-1, 1] interval by max Vdc supported value.
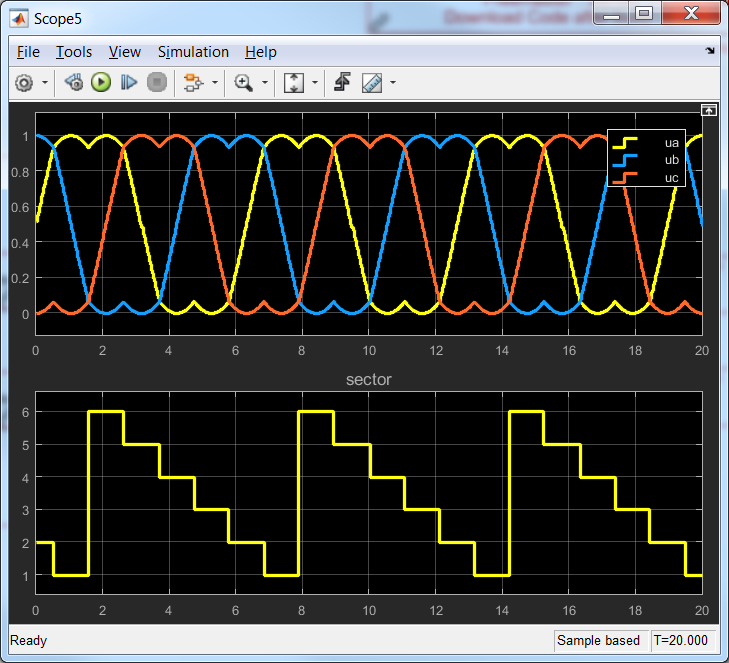
Using Ualpha and Ubeta, the stator voltage vector Us is constructed with the appropriate combination of inverter switching patterns. Based on the actual value needed for the stator voltage vector Us to control the rotor position, the 6 inverter switches must be controlled: ON or OFF for an amount of time - duty cycle/factor.
So, the output of the SVM block represents the PWM duty cycle to control the inverter switches/transistors. Since the duty cycle represent the relative time of the transitor to be ON/OFF the only meaningful values are between [0 and 1]
And finally:
... the output of the SVM, should it be exactly changing from 0 to 1 in order to have proper operation of the power stage ? or it could be changing between any [min, max] values inside [0,1]!
Yes, it should always be between [0=OFF ... 1=ON] interval since it is a PWM duty cycle value. Note that SVM also implement the 3rd harmonic injection to increase the actual phase voltage from Vdc/2 -> 0.155* Vdc/2 (see the curly waveform) - but that is a different topic.
Attached is a Simulink model where you can play with the SVM block and MPC5744P Toolbox.
Hope this helps clarifying some of the concerns around this special block.
Original Attachment has been moved to: SVM_FLT.slx.zip