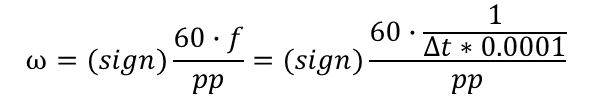- NXP Forums
- Product Forums
- General Purpose MicrocontrollersGeneral Purpose Microcontrollers
- i.MX Forumsi.MX Forums
- QorIQ Processing PlatformsQorIQ Processing Platforms
- Identification and SecurityIdentification and Security
- Power ManagementPower Management
- MCX Microcontrollers
- S32G
- S32K
- S32V
- MPC5xxx
- Other NXP Products
- Wireless Connectivity
- S12 / MagniV Microcontrollers
- Powertrain and Electrification Analog Drivers
- Sensors
- Vybrid Processors
- Digital Signal Controllers
- 8-bit Microcontrollers
- ColdFire/68K Microcontrollers and Processors
- PowerQUICC Processors
- OSBDM and TBDML
-
- Solution Forums
- Software Forums
- MCUXpresso Software and ToolsMCUXpresso Software and Tools
- CodeWarriorCodeWarrior
- MQX Software SolutionsMQX Software Solutions
- Model-Based Design Toolbox (MBDT)Model-Based Design Toolbox (MBDT)
- FreeMASTER
- eIQ Machine Learning Software
- Embedded Software and Tools Clinic
- S32 SDK
- S32 Design Studio
- Vigiles
- GUI Guider
- Zephyr Project
- Voice Technology
- Application Software Packs
- Secure Provisioning SDK (SPSDK)
- Processor Expert Software
-
- Topics
- Mobile Robotics - Drones and RoversMobile Robotics - Drones and Rovers
- NXP Training ContentNXP Training Content
- University ProgramsUniversity Programs
- Rapid IoT
- NXP Designs
- SafeAssure-Community
- OSS Security & Maintenance
- Using Our Community
-
-
- Home
- :
- Model-Based Design Toolbox (MBDT)
- :
- Model-Based Design Toolbox (MBDT)
- :
- Re: Module 8: Speed Control
Module 8: Speed Control
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Module 8: Speed Control
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
| Electric Motors in Automotive – Speed Control Is Everywhere |
INTRODUCTION
Permanent-magnet synchronous motors (PMSM) are widely used for many automotive applications due to their high torque, high power density and high efficiency. In a typical modern car there are numerous functionalities that are driven by PMSM type of motors and most of these functionalities need to operate at various speed levels that must be controlled precisely. Besides car industry, there are many other areas of industrial control that require the motor speed control capabilities to ensure a proper system operation: just think about a bottling factory conveyor belt system, or an airport walkway, or why not an car assembly line. All these would not be possible without an appropriate way to control various motors speed.
The main topic of this 8th module of 3-Phase PMSM Control Workshop with NXP's Model-Based Design Toolbox is about PMSM Speed Controllers and how to build a reliable control system based on FOC that will perform under various load conditions and should be able to reject external disturbances that might occur in such systems.
The purpose of this article is to build a closed loop speed control system based on position sensor feedback. The user will be able to set a speed reference and the control system implemented with the help of S32K14x MCU will drive the PMSM to the command set point and will have to maintain it there until the user command changes. The control system shall deal with all system disturbances automatically by adjusting the FOC flux and torque commands to keep the rotor in synchronism and to operate at its optimal operating points.
In this module we are going to describe how to:
- Implement a speed and position estimator based on low-cost Hall effect sensors;
- Regulate the motor speed by implemented a dedicated PI control system;
- Interconnect Speed and Torque (developed in Module 7: Torque Control ) modes of operations;
In Fig. 1, which represent the global application mapping diagram as discussed in Module 3: System Partitioning , are shown the new hardware blocks that are going to be configured and used to perform the PMSM Sensored Speed Control highlighted in green relative to the ones already configured so far in the previous modules of this workshop. This time we are going to configure the GPIO to generate interrupts each time the Hall sensors change their state allowing us to compute the rotor position and motor speed using a simple estimation approach based on counting the time between Hall transitions.
Furthermore, we are going to reuse and enhance the model developed in Module 7: Torque Control . The interactions between host PC and hardware will be done via OpenSDA serial communication that will be used to download the code generated from MATLAB and to visualize various control signals with FreeMASTER. In addition, the user can start and control the motor speed from the SW2 and SW3 push buttons that are present on the S32K144 Evaluation Board|NXP . A three color LED will be used to signal the control states and faults.
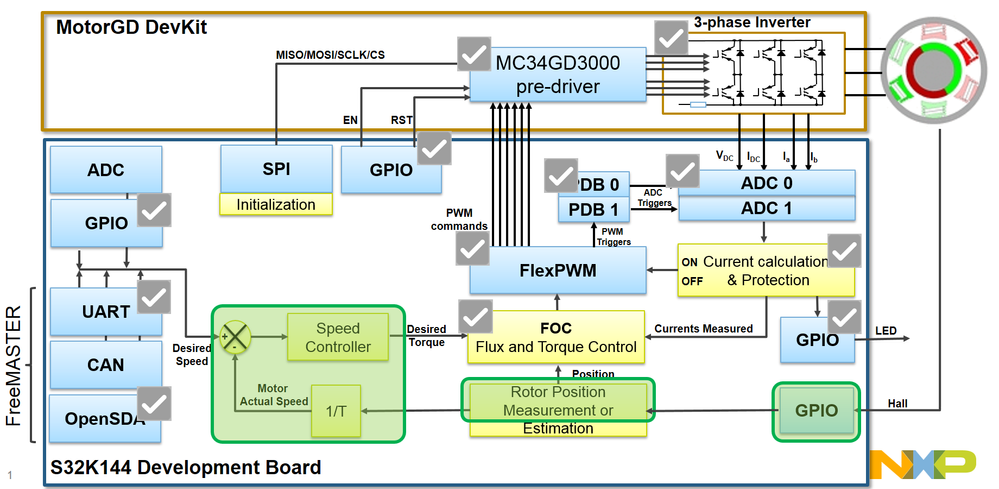 |
| Fig. 1: Application Mapping - new HW & SW modules used for Sensored Speed Control are highlighted in green |
This example uses the HALL Sensors to implement a simple position estimator. The usage of HALL Sensors should not be mistaken with 6-step commutation technique used to control the BLDC. In this case the HALL sensors are used just for estimation and correction of the electric angle used for FOC
CLOSED LOOP SPEED CONTROL SYSTEM
The Speed Control system requires the actual/real motor speed in order to perform the calculation for finding the appropriate value for the Torque reference (Iq*) used to accelerate or decelerate the PMSM rotor so that the real speed is maintained as closed as possible within the user specified range.
In Fig. 2, is shown the block diagram of a typical closed loop speed control system proposed for implementation. The control system is made of two cascaded loops that use information about currents and rotor position to regulate the PMSM rotor speed to a desired set point.
 |
| Fig. 2: Closed loop speed control system - Block Diagram |
The Field Oriented Control shown in Fig. 3, is computed in the FAST CONTROL LOOP block that is executed based on a ADC triggers at each 100 microseconds. This subsystem receives the reference values for currents in Q (torque) and D (flux) axis and use as feedback the Ia,Ib and Ic currents measured from the ADC that are transformed from the fixed reference frame (abc) to the orthogonal rotating frame (dq) based on the angle θ provided from position sensors and PARK and CLARKE transformations. The FAST CONTROL LOOP outputs via the Space Vector Modulation technique the PWM duty cycles commands that control the 3-phase inverter which applies the corrective voltages directly to the PMSM windings.
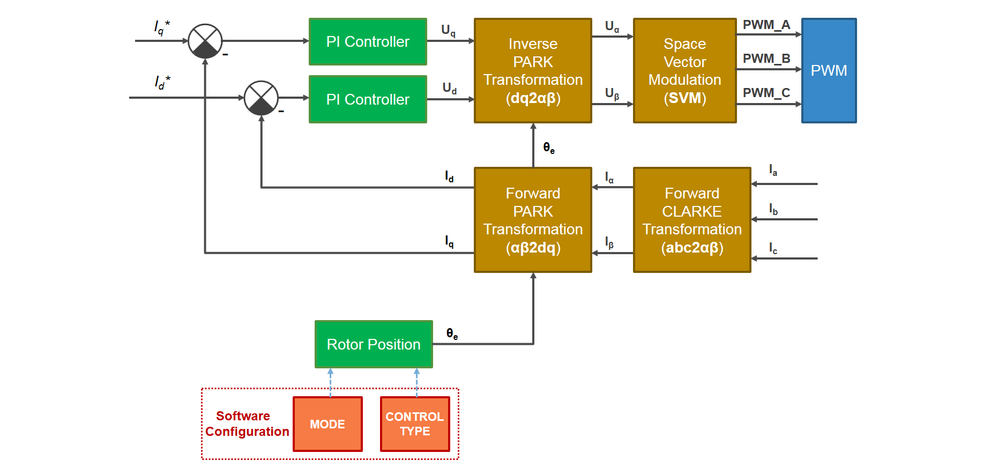 |
| Fig. 3: Field Oriented Control - Block diagram |
For flexibility, the actual electric angle θe used in FOC calculations is derived from the position sensor measurements and estimations based on application software configuration global variables: MODE and CONTROL TYPE.
The CONTROL TYPE global variable allows users to choose between:
- SPEED CONTROL = 1 that performs the closed loop speed control based on sensor feedback
- TORQUE CONTROL = 0 that performs the control system designed in Module 7: Torque Control
The TORQUE CONTROL operation is very important at this time because it will allows us to perform various tests with the speed and position estimator prior of closing the speed control loop.
The second global variable, MODE is generated internally by the software algorithm and it is used to control the motor startup process and zero crossing during change of rotation direction. Since we are dealing with an estimator we need to cope with low speed ranges and 0 crossing when changing the motor speeds from clockwise (CW) to counter clockwise (CCW) directions. This variable has three possible values (see Fig. 27 for a graphical representation):
- FORCE MODE = 0 where the motor is control in open loop with an imposed electric angle reference
- TRACKING MODE = 1 where the motor is still control in open loop but the speed controller will act in parallel to charge the integral part in order to deal with handover from open to closed loop transition
- SENSOR/SENSORLESS MODE = 2 where the motor operates as a closed loop system and the electrical angle is derived from the actual rotor position sensors.
We will discuss about the importance of these modes in the next workshop modules where we will focus on SENSORLESS control system.
Furthermore, the Toque (Iq*) and Flux (id*) references are computed in the SLOW CONTROL LOOP block that is triggered at each 1 millisecond based on the same ADC events.
The block diagram of the SLOW CONTROL LOOP is shown in Fig. 4. As can be seen, the same software configuration based on MODE and CONTROL TYPE is used here as well to select between TORQUE and SPEED control types. The speed commands ω* are received via the UART or from on board push buttons and feed into a PI controller together with the actual rotor speed feedback ω. The PI Speed Controller implements a standard Simulink PI parallel controller that takes as input the error between the speed set point and the actual rotor speed and computes the appropriate torque command Iq* that compensates for the speed error.
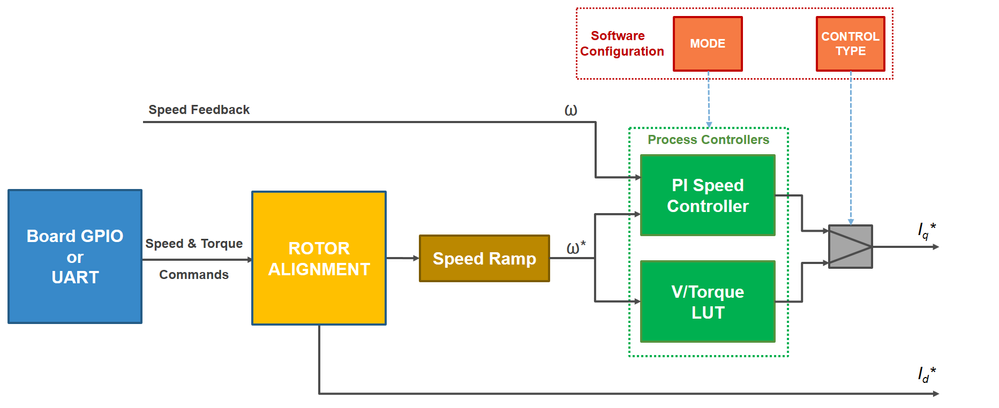 |
| Fig. 4: Closed Loops Speed Control - Block diagram |
As can be seen in Fig. 2, Fig. 3 and Fig. 4 the key information needed for speed closed loop control is the actual rotor position information. Therefore, lets see how can we obtain such information.
SPEED & POSITION ESTIMATOR
In general for an accurate closed loop speed control system we need to have a dedicated position (optical encoder or resolver) or speed (tachometer) sensors that can provide relative or absolute rotor position information. Unfortunately many of these sensors are expensive and require additional dedicated hardware and PCB space for signal conditioning or may of them need dedicated software routines to allow data read outs.
Fortunately, most of the motors can be equipped with low resolution Hall-effect sensors that are very cheap and widely used in many PMSM based applications. In general three Hall sensors are used in one PMSM to provide the rotor position with a coarse resolution of 60 electrical degrees. A detailed description about how Hall-effect sensors operates can be found in Motor Control Class: Lecture 5 - Hall Sensors
In case of the DevKit MotorGD the Hall sensors are connected via JP1 connector on the motor shield as shown in Fig. 5. The JP1 connector provides 5V power supply to the motor Hall sensors and reads back the digital signals in range of 0 - 5V.
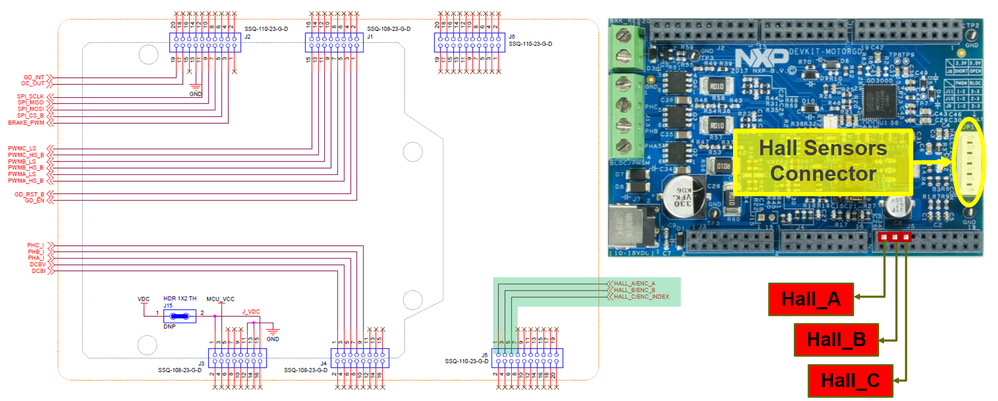 |
| Fig. 5: DevKit MotorGD pins used for Hall sensors |
The signals from Hall sensors are then sent to the S32K144 Evaluation board via the J5 header as shown in Fig. 6 and the S32K MCU will read those from the PTA15, PTA16 and PTA1 digital inputs pins.
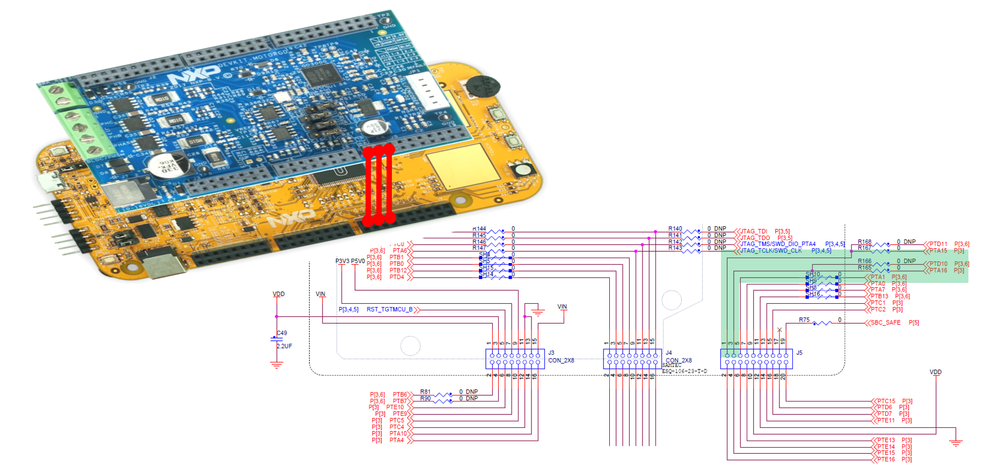 |
| Fig. 6: S32K144 Evaluation Board MCU Signal Assignment |
Getting the actual values of the Hall signals is a piece of cake when using the NXP Model-Based Design tools. Using a simple digital input block you can read each hall signal individually and store it in a global variable as shown in Fig. 7.
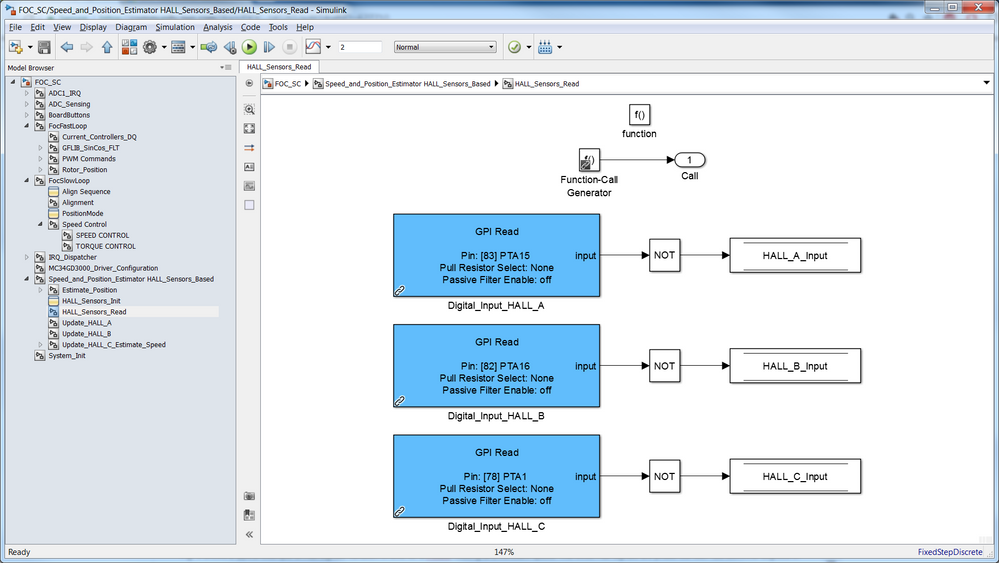 |
| Fig. 7: Simulink model for reading the Hall Sensors with S32K14x MCU |
On S32K14x Evaluation Board these signals are inverted. To get the same logic value as the true Hall input we need to invert the acquired value in software.
Using the Simulink model shown in Fig. 7 we can read the Hall signals variation in time for a PMSM rotating at a constant speed. Fig. 8 shows the three Hall signals that are phase out with 120 electrical degrees in between each other while each hall signal is ON/OFF for 180 electrical degrees.
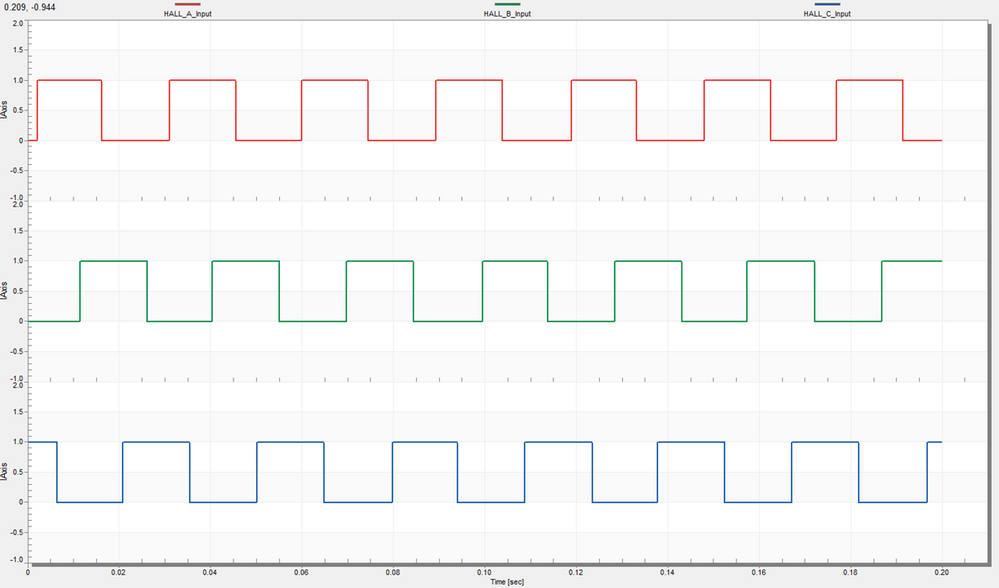 |
| Fig. 8: HALL sensors signals |
Based on these considerations, it is easy to understand that for each 360 electrical degrees (THETA) we will have six Hall sensor transitions as shown in Fig. 9. These six transitions give us the possibility to measure the position of the PMSM rotor with an accuracy of 60 electrical degrees for any speed range.
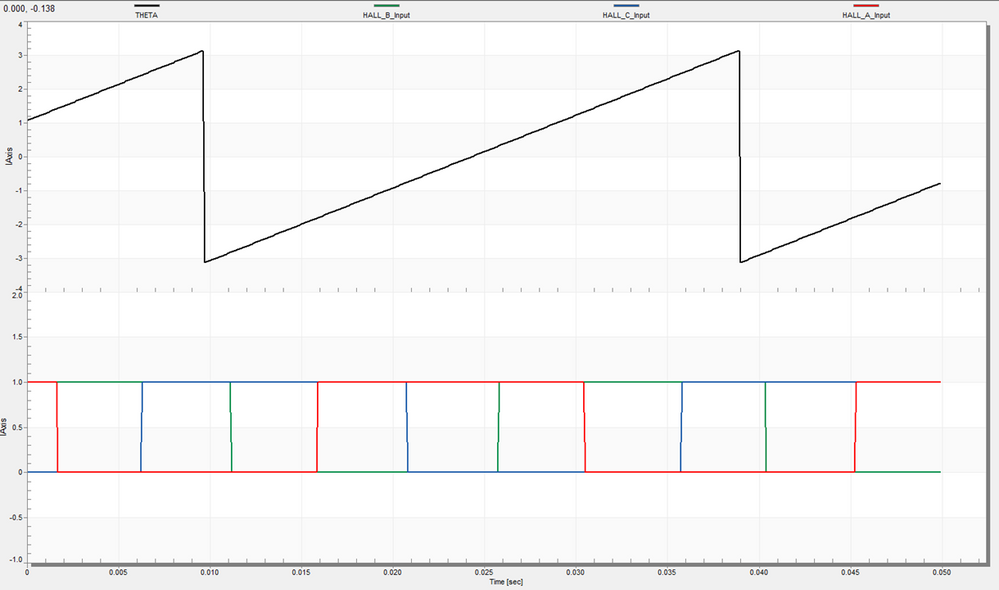 |
| Fig. 9: Hall sensors transitions versus one complete electrical rotation (-pi: pi) radians |
Speed Estimation Based on Hall Sensors Transitions
Since we know how many radians are between two consecutive Hall sensors transitions, we can easily compute the speed of the motor as:
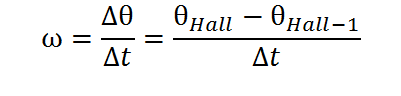 | Eg. 1 |
Therefore, reading the value of a timer/counter on each hall transition should give us an accurate information about how fast the rotor is spinning, right ?
In Fig. 10 we have captured such use-case. On the top of the figure we have the Hall sensors variation captured as a Hall sSector representation in decimal form and on the bottom we have the timer values for each Hall sensors transitions. In this capture you can see that even if the motor is commanded to spin in torque control at constant speed the time counted between consecutive hall transitions presents a variation.
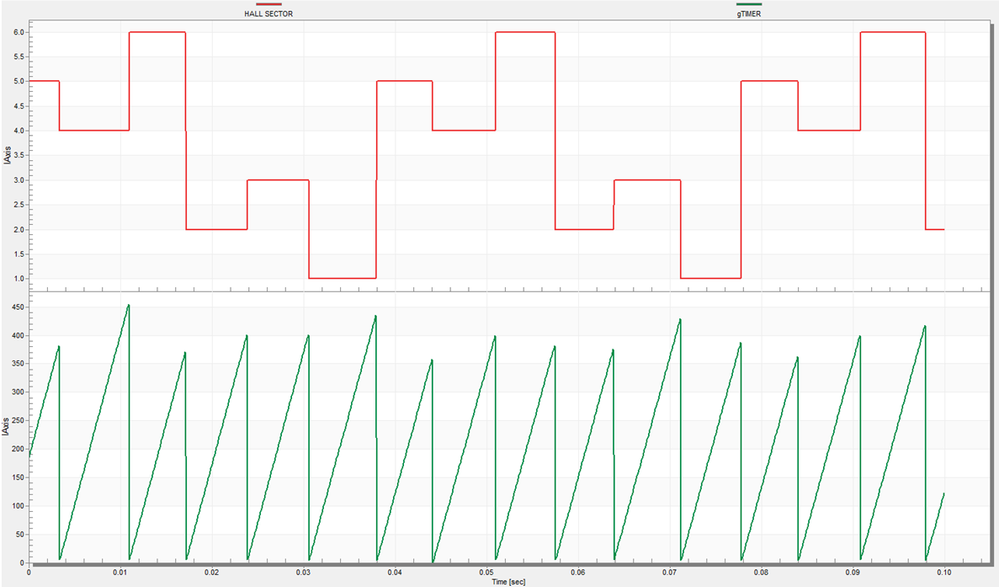 |
| Fig. 10: Hall sector change timings |
This variation is mainly cause by the undefined installation error of the three hall sensors which are not at a perfect 120 electrical degrees apart of each other. If we would try to build a speed estimator based on this approach we will have to deal with a lot of variations that are induced by this poor mechanical hall installation that might vary from one motor to the other.
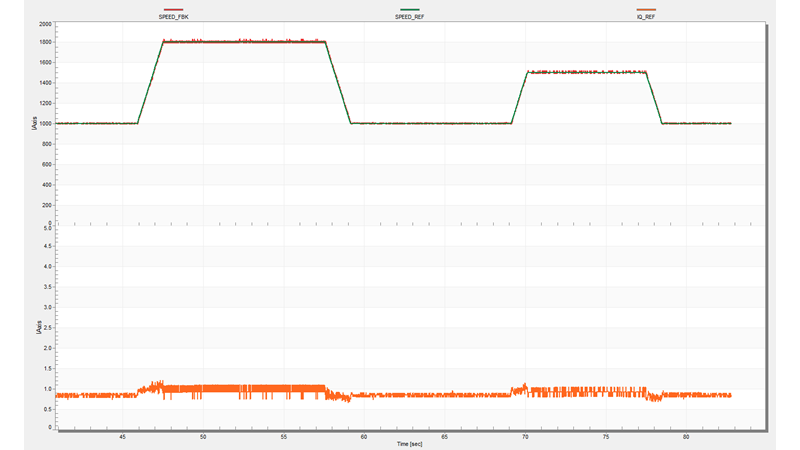
In Fig.11 is shown the speed estimation results in case of counting the time between each hall sensors transitions. In this case the motor was commanded to spin in Torque Control at a constant 1000 rpm demanded speed using open loop control. As you can see the estimated speed (SPEED_FBK blue) has a large variation around the set point.
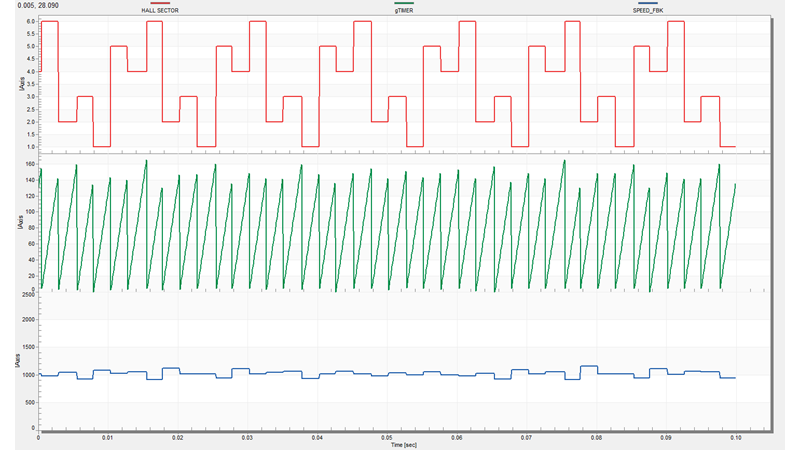 |
| Fig. 11: Speed estimation by counting the time between each hall sensor transitions |
Such speed estimation signal may be filtered out but to smooth down such large variations it might required a large sample data as history and that may introduce phase delays in the final closed loop control system that may create control system instability. Therefore it must be a different way - a better one!
After analyzing the system response we have reached to the conclusion that would be better to count the time between a single hall transitions over 360 electrical degrees. This way we can get rid of additional sources of errors that might affect the speed estimator like:
- wrong placement of the hall sensor near a stator coil that might interfere with rotor magnetic flux
- misalignment of rotor permanent magnets that might influence the North vs South magnetic poles spread
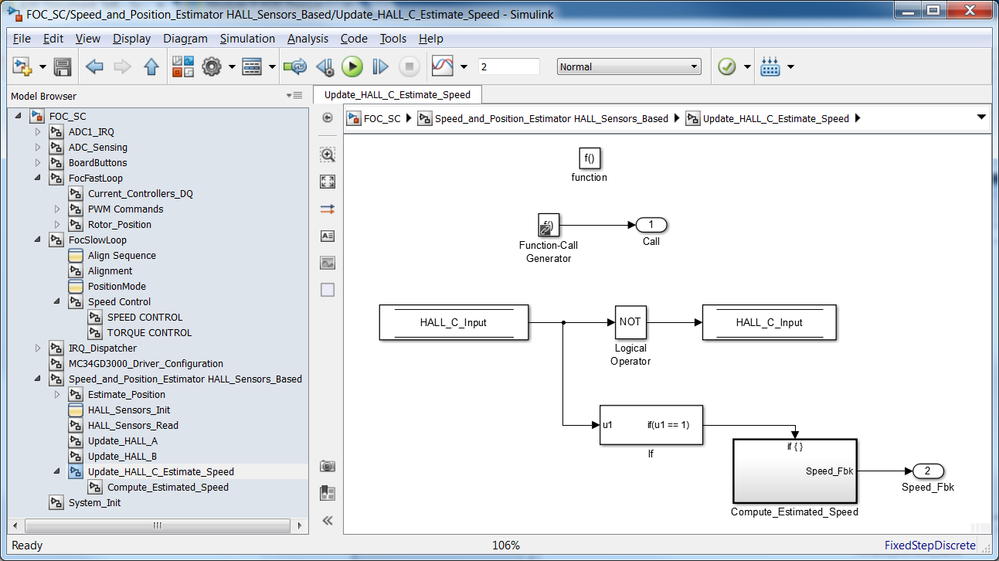
The new Simulink model that is supposed to handle this scenario is shown in Fig. 12. Each time there is transition from HIGH to LOW on the HALL C (is has been selected since from PCB point of view it is all the time routed to the MCU) the new estimated speed is getting computed.
|
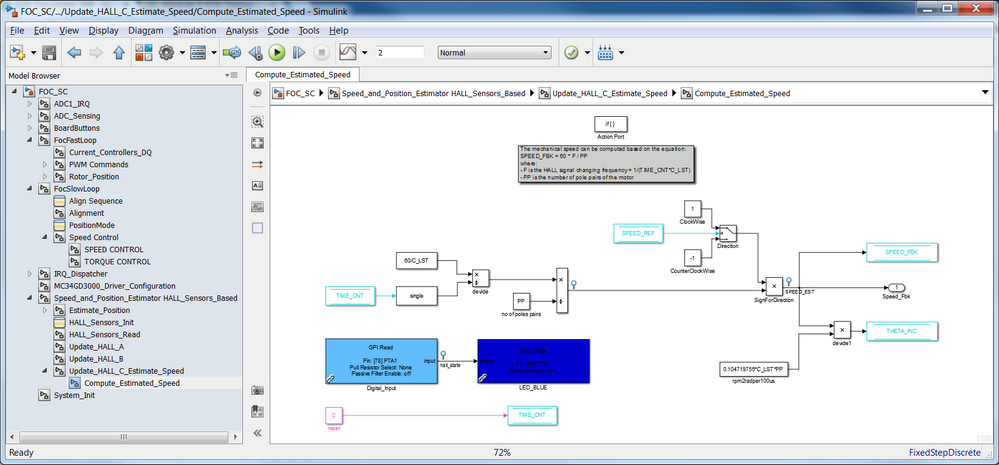
The formula implemented in the Compute Estimated Speed block is based on:
where:
| Eq. 2 |
Using this approach we can estimate the actual motor speed far more cleaner that before. Fig. 13 shows the estimation results in the same conditions as the one from Fig. 11.
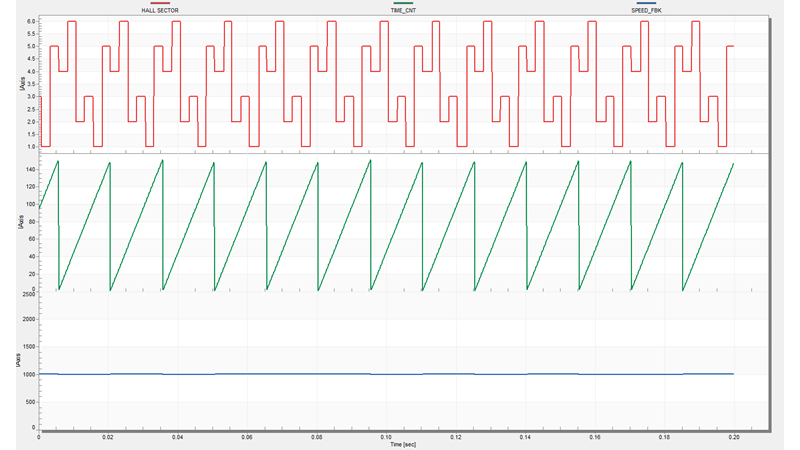 |
| Fig. 13: Speed estimation by counting the time between one Hall signal transitions over 360 electrical degrees |
The dynamic results of the Speed Estimator are shown in Fig. 14 and Fig. 15 for startup and change of direction with zero crossing.
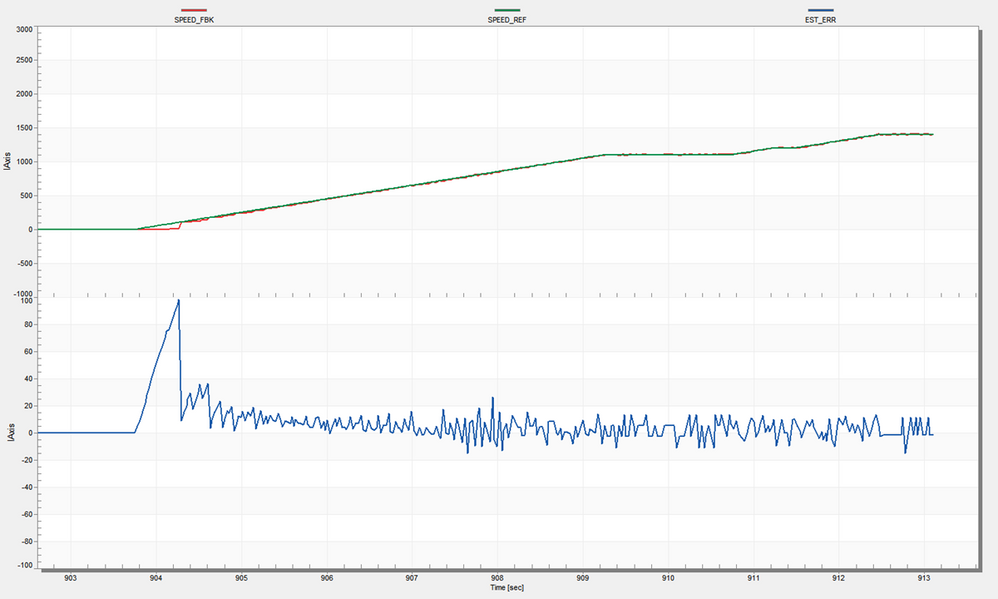 |
| Fig. 14: Top: Reference (green) vs Estimated (red) Speeds, Bottom: Speed error between the reference and estimated speeds during motor startup |
As can be seen, we have an expected larger error at startup until the motor starts to move constantly. Then during acceleration and steady state regime the error between the reference and estimated values are quite small +/-20 rpm which I think is quite good for this kind of approach relative to solution costs.
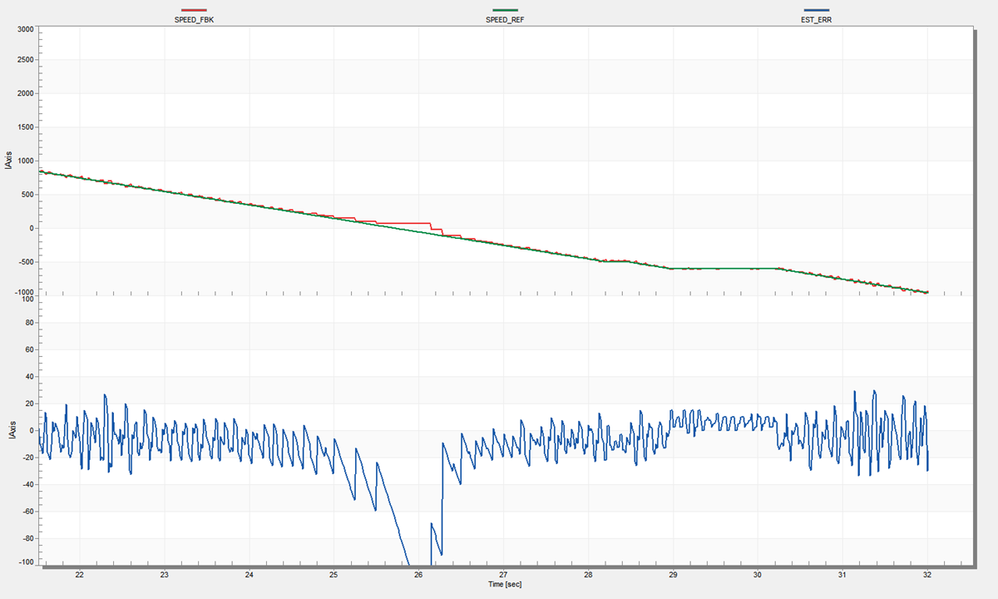 |
| Fig. 15: Top: Reference (green) vs Estimated (red) Speeds, Bottom: Speed error between the reference and estimated speeds during change of direction with zero crossing |
At this point I think we can say the speed estimator based on a single Hall sensor signal transitions is accurate enough for our purpose. The next question that rise now is: how to obtain the electrical angle that is used for FOC transformations that ultimately controls the rotor position?
Position Estimation Based on Hall Sensors Transitions
For FOC, the 60 electrical degrees resolution is not good enough to control the rotor position using sinusoidal control approuch. We will need to find a way to improve this accuracy in order to be able to reuse the Hall sensor information for PMSM sinusoidal control.
With the PMSM rotating at a constant speed like Fig. 16 shows, the Hall sensors values change regularly.
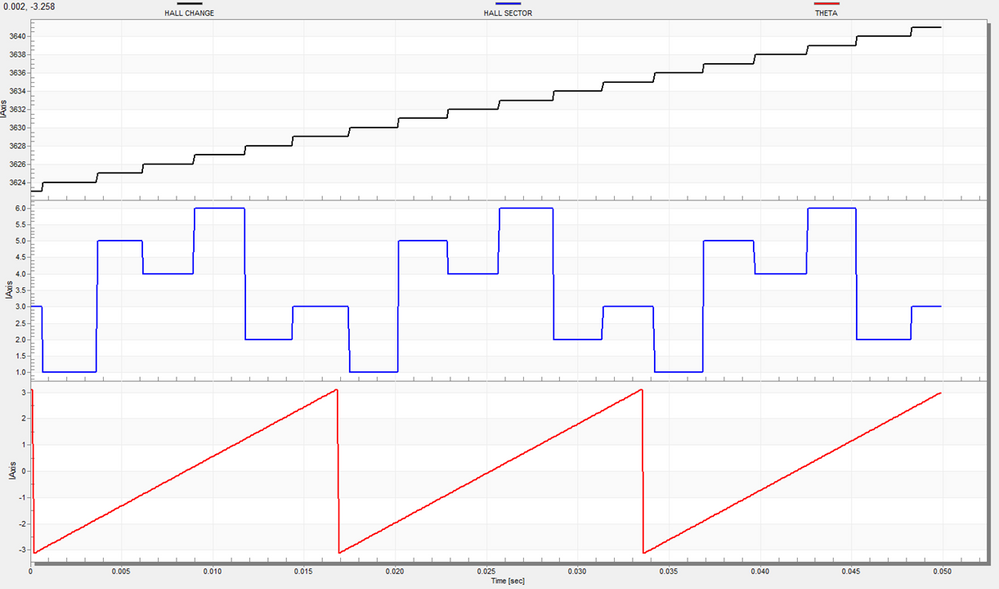 |
Fig. 16: Hall sensors changing at constant speed - comparison between hall change (black), hall sector (blue) and open loop electric angle (red) |
Any changes of Hall sensors value could be captured by the MCU via dedicated GPIO Interrupts and then the software application could reads the three Hall sensors values to judge in which section edge the rotor is. The Simulink model that implements the Hall sensors change capture is shown in Fig. 17. As can be seen, dedicated GPIO ISR blocks are used to trigger a subsystem execution each time the Hall sensor changes its state LOW to HIGH or HIGH to LOW.
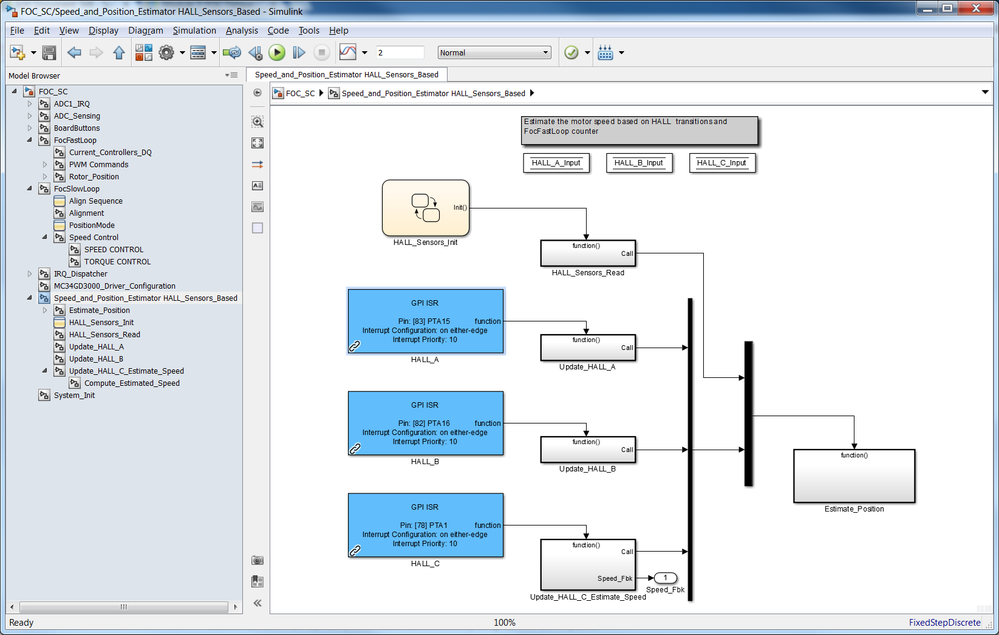 |
| Fig. 17: Simulink model for capturing the Hall sensors transitions |
For instance, when the MCU captures a Hall sensor value changing from 110 to 010 then it is easy to know that θ is equal with 60 electrical degrees apart of phase A magnetic axis. The whole 360 electrical degrees spectrum can be divided into six areas, each one spreading over 60 electrical degrees. This concept was discussed in Module 4: Space Vector Modulation during Space Vector Modulation.
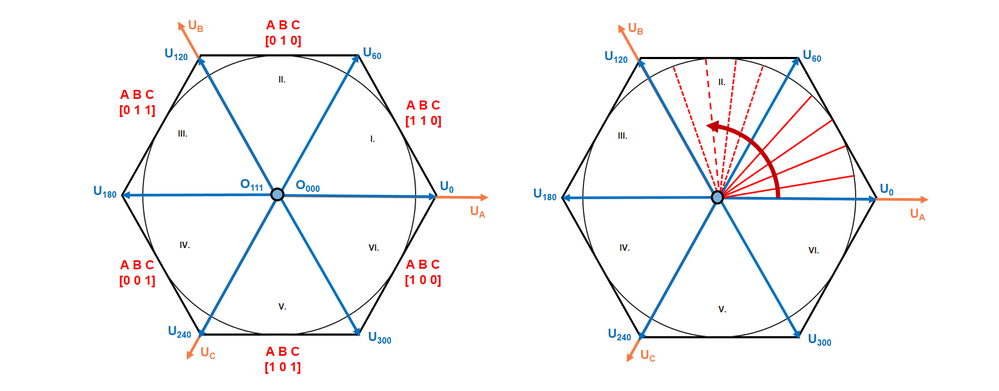 |
| Fig. 18: Hall sensors states vs. PMSM rotor angle |
Using only the six Hall sensors transitions we can build a simple model to estimate the rotor position with a resolution of 60 electrical degrees as shown in Fig. 19.
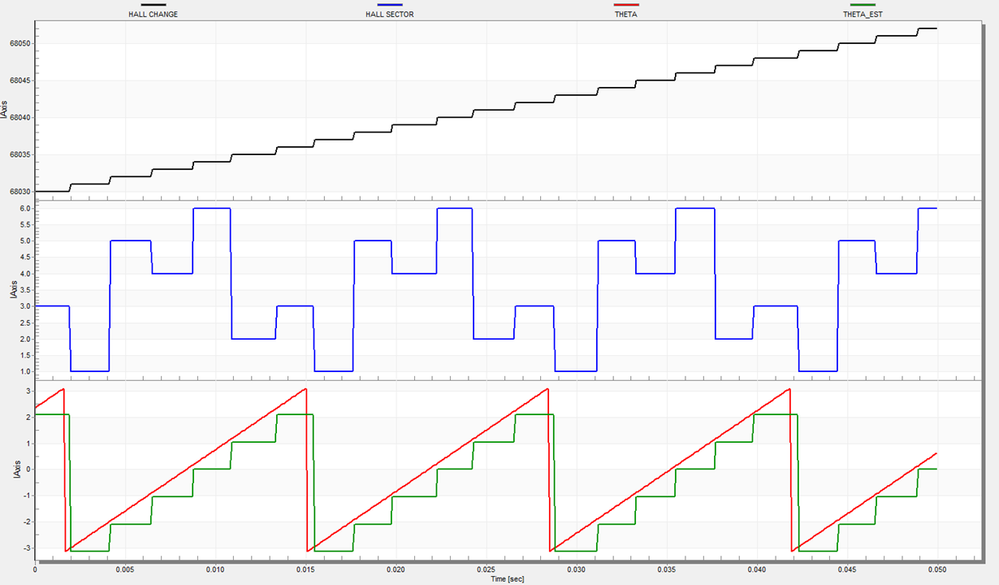 |
| Fig. 19: Coarse estimated rotor position (green) vs. Ideal rotor position (red) when using Hall sensors transitions |
But how to estimate the rotor angle within these six sections is an important problem which can be solved by using the estimated speed. Looking at the Fig. 18, we can see that the rotor position can be approximated quite precisely in case we know how fast the PMSM rotates.
In FOC algorithm, the rotary speed of last 360 electrical degrees section is used to predict the rotor position for the next 60 electrical degrees section now which of course implies that the speed used until next Hall changes is not the real speed at the present moment.
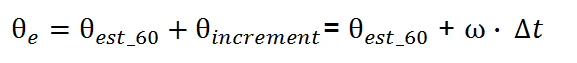 | Eq. 3 |
The predicted rotor angle may contains errors if the motor speed is not constant, (e.g.: the PMSM is accelerating or decelerating). So the electrical angle estimation result may have some deformity when the PMSM speed is fluctuating.
The coarse estimated rotor position shown in green within Fig. 19, can be easily computed with a simple SWITCH in Simulink as shown in Fig. 20.
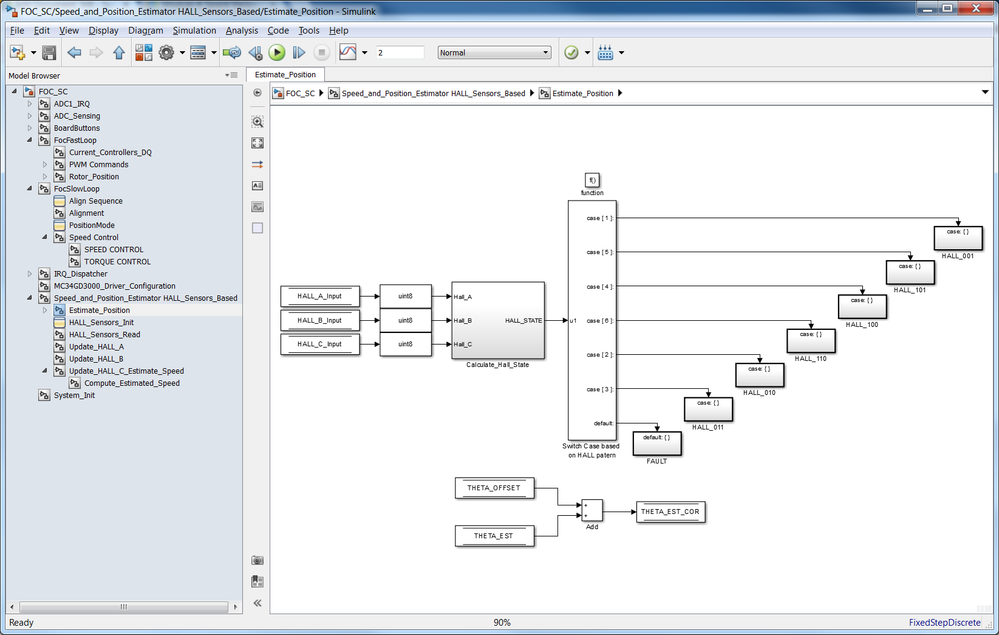 |
| Fig. 20: Simulink model used to compute the coarse rotor position with 60 electrical degrees resolution based on Hall sensors transitions |
This is a simple implementation that assumes a specific Hall switching pattern as shown in Fig. 19. For any other motor this part of the model must be updated.
The position angle increment computation is shown in Fig. 12 and is computed in the same time with the estimated speed as a simple multiplication with a scaling factor from rpm to rad/s and of course the sampling time of the fast loop
where the Hall transitions timer is incremented.
Applying all these knowledge we can compute a more accurate rotor position based on actual Hall sensors transitions and the estimated speed of the PMSM. Fig. 21 shows a comparison between the ideal rotor position (THETA) and the predicted position (THETA_CORRECTED) based on the algorithm discussed above.
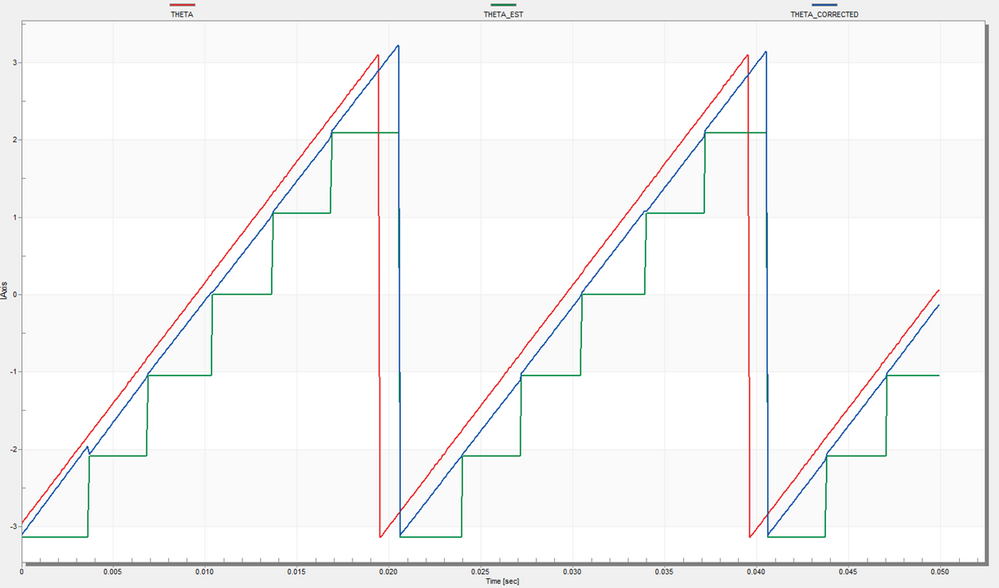 |
Fig. 21: PMSM rotor position comparison: (red) represents the ideal rotor position which is imposed in open loop Torque Control (green) represents the coarse estimated rotor position with a 60 electrical degrees resolution based on Hall sensors transitions (blue) represents the rotor predicted position based on Eq. 3 that includes the speed prediction |
If we check the Fig. 21, we can spot a few things that needs to be addressed:
- the predicted position (blue) must be scaled to be withing the (-pi:pi) radians range.
- compensate the offset between ideal (red) and predicted (blue) positions
The first issue can be easily addressed in software and Fig. 22 shows how to deal with such aspects in Simulink.
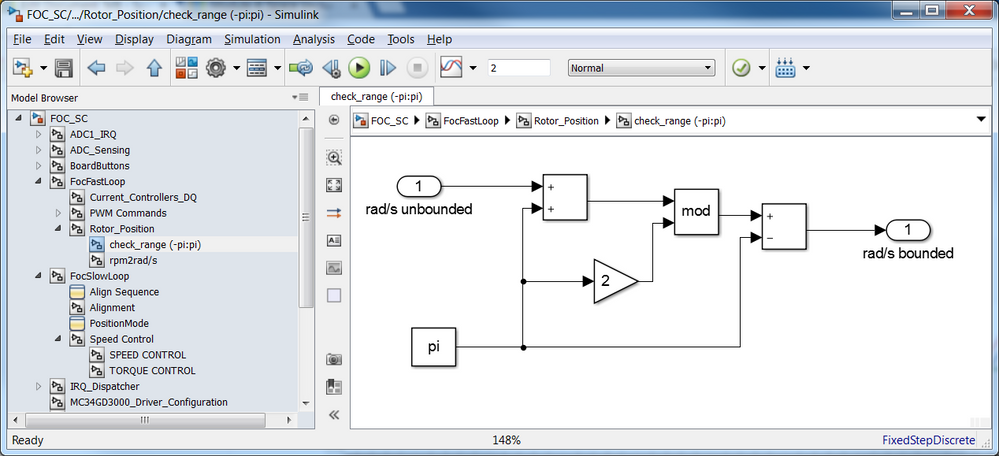 |
| Fig. 22: Bounding the estimated rotor position to (-pi:pi) radians using standard Simulink blocks |
Regarding the second issue, the things are a bit more complicated than they seems and to explain it, we need to have a deeper understanding of the PMSM internals: phase voltage, back-emf and Hall sensor mounting. Lets discuss all these in the next section.
Phase Lag and Phase-Angle Advance Compensation
One of the most important control system design challenges is the phase lag between the commanded phase voltage impose via SVM and the resultant sine-wave phase current for that naturally occurs in an PMSM/BLDC motor. The PMSM can operate satisfactorily, but the overall efficiency will be reduced (as shown in Fig. 39), defeating much of the purpose of implementing a FOC control scheme that by definition should drive the motor at its optimal operating point.
The source of this inefficiency is not the phase lag between motor phase voltage and phase which some might think but rather the phase lag between phase current and the induced back-EMF voltage as it is shown in Fig. 23.
The Hall sensors are mounted in such way that when the induced back-EMF reaches its maximum value a Hall transition will happen. In this case, since we can measure directly the back-EMF with our model, it is safe to assume that back-EMF is synchronized with Hall transitions.
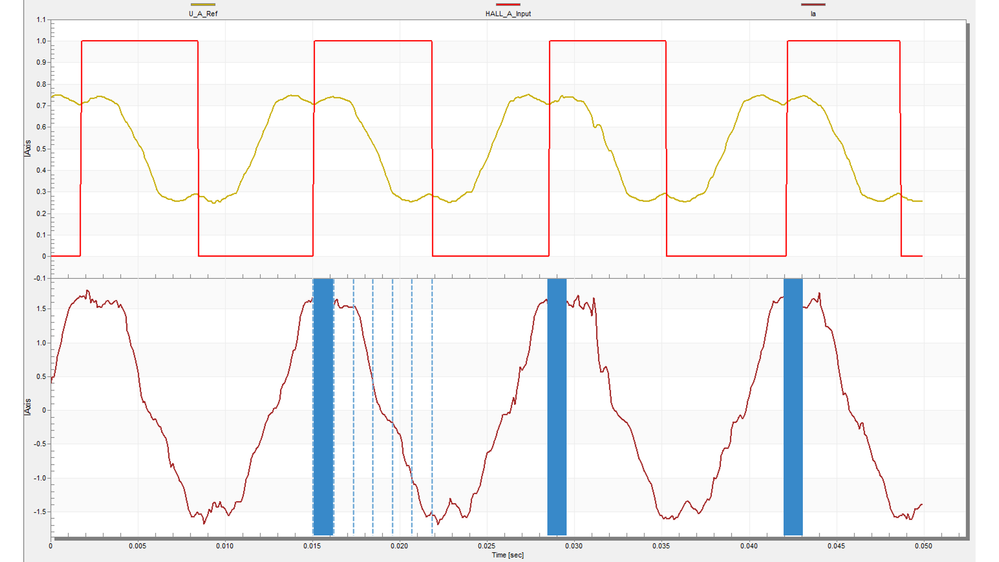 |
| Fig. 23: Phase lag between phase voltage (U_A_Ref) and phase current (Ia) and the Hall A transitions that are synchronized with back-EMF in phase A |
In order to eliminate this lag between the back-EMF (Hall A) and the phase current (Ia) we need to introduce a phase-angle advance to the sinusoidal drive current to ensure its peak coincides with that of the back EMF (Hall transition). This phase-angle advance can be easily deducted based on the FreeMASTER recorded captures and in my case it seems to be 1/6 from a Hall half period (the dotted areas) which can be translated in a pi/6 radians or 30 electrical degrees.
In general, the phase-angle advance is typically set to increase linearly with the phase command voltage, which determines the motor speed. Since our scope is to introduce general concepts and show how to implement them with Simulink rather than building a dedicated speed control system targeted for a particular motor - in this module we are going to use a constant electrical angle offset to compensate for this lag and drive the motor to its peak efficiency within a specific speed range.
Depending on your application you might need to consider this aspect.
The compensation of the electrical angle (Fig. 24) for clockwise and counter clockwise direction is implemented on the slow control loop and uses constant offsets that are added to the corrected electrical angle as shown in Fig. 21.
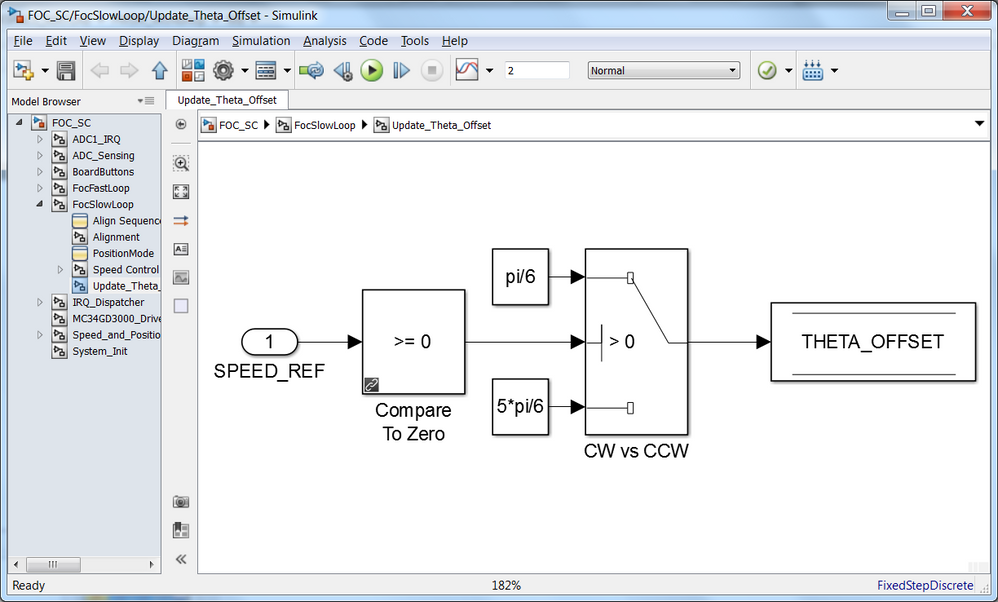 |
| Fig. 24: Electric angle offset calculation for phase lag compensation |
By using all these tricks we should be able to predict the rotor position quite accurately in both clockwise or counter clockwise directions as shown in Fig. 25 and Fig. 26.
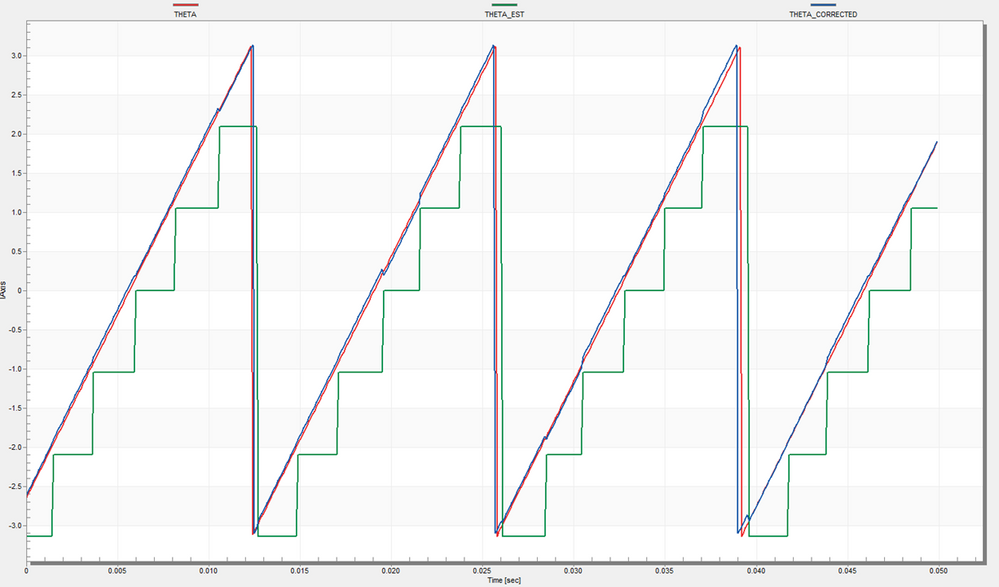 |
| Fig. 25: PMSM rotor position corrected (blue) with phase-angle advance of 30 electrical degree for clockwise direction |
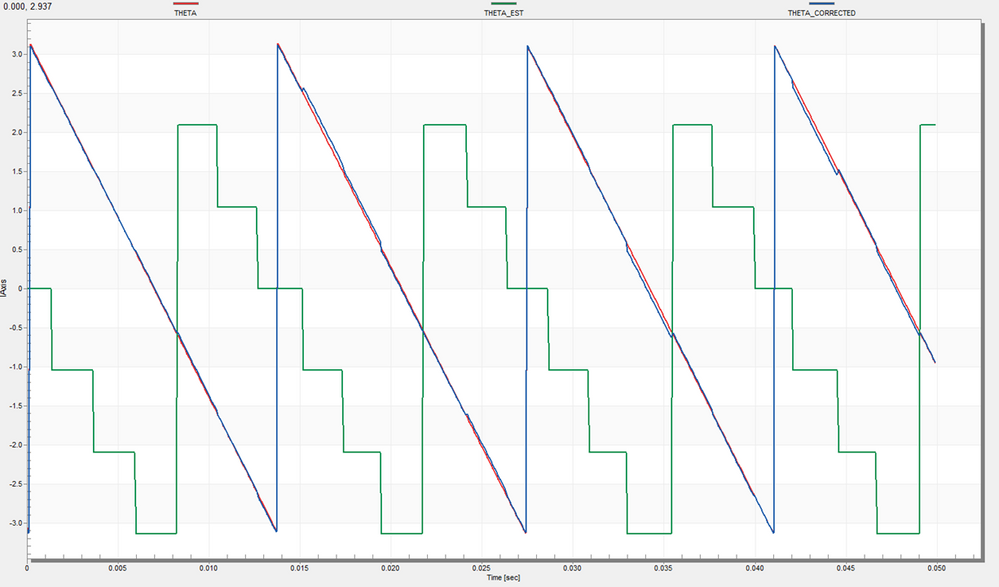 |
| Fig. 26: PMSM rotor position corrected (blue) with phase-angle advance of 30 electrical degree for counter clockwise direction |
Fig. 26 shows a 180 degrees angle shift between the coarse angle obtained from Hall sensors (green) and the electrical angle corrected due to the mechanism used for calculations. To keep the same algorithm implementation for both directions, the corrected angle is shifted in software with (pi-pi/6) radians
As can be seen in both Fig. 25 & 26, there is a small jitter present on the predicted rotor position which is due to keeping the same angle increment over 360 electrical degrees and small variations with the estimated speed, but that should not be an issue for the control system.
Overall, taking into account the accuracy of predictions for both speed and position on one hand side and the cost of such basic type of sensors we can conclude at this point that this kind of method is quite suitable for motor control applications.
SPEED CONTROL
Before we start to implement the speed controller that take governance over the system, we need to clarify a few things. As has been demonstrated before (Fig. 14 &15) such speed and position estimators work quite well in steady state regime and pose some design challenges when dealing with dynamic regimes due to their intrinsic algorithm that use previous states as a base for estimating the new values.
Taking into account these factors we need to consider:
- startup process - where due to lack of Hall pulses is quite difficult to accurately predict the rotor position and that might lead to oscillations an possible lost of synchronism.
- zero crossing - is somehow similar with startup process in terms of missing the accuracy in hall transitions but we also need to consider the behavior of the PI type controllers that needs to empty the integral part in order to change direction. To have a smooth transition thru 0 we will need to offload the integral sum or at least to provide a mechanism to allow the controller to accommodate the change in directions.
In industry there are two main techniques to cope with such situations:
- BLDC Startup - at low speed the control is switch from FOC (sinusoidal) to 6-step commutation BLDC (trapezoidal) and only when the speed is high enough the control is switch back to FOC sinusoidal. Such type of control adds additional software complexities since we need to change the PWM strategy on the fly.
- Force Startup - for a selected speed range the motor is driven in open loop by imposing a constant electric angle increment. The transition to closed loop is then made via a second region called Tracking Region where the Speed Controller works in parallel with the Open Loop control allowing enough time to accumulate the integral term in order to have a smooth transition from open to closed loop.
Depending on your application requirements you may choose between one or the other method. For this module we are going to implement the Force Startup since it is more common and less complex than the BLDC Startup. If you are interested in BLDC control theory you may want to check BLDC Motor Control with Model Based Design
Fig. 27 shows the speed range partitioning for the Force Startup approach.The speed limits are available for changing in the Model Workspace associated with the Simulink Model File.
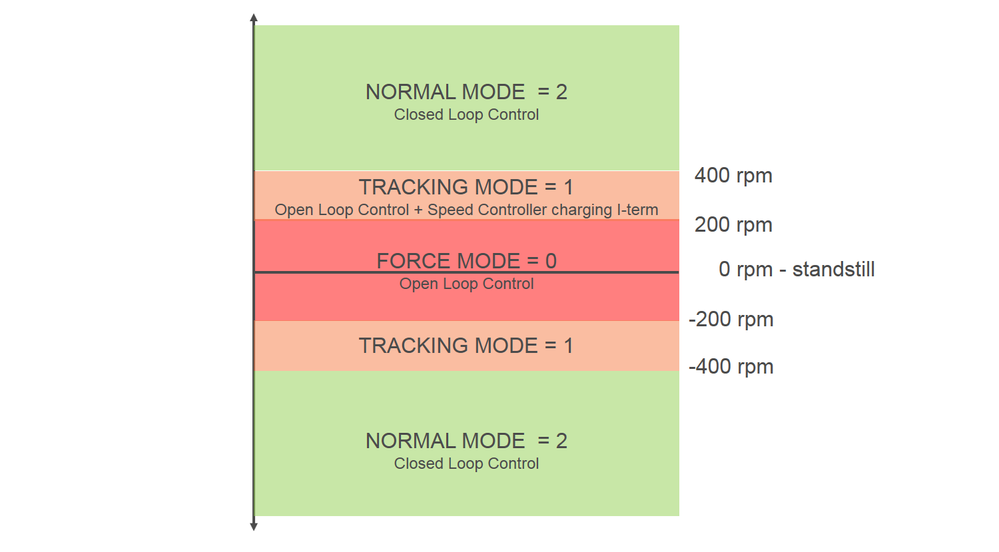 |
| Fig. 27: Force Startup speed zones and speed limits between transitions |
The Simulink model is built to take into consideration these transitions and change the Speed Feedback (SPEED_FBK) and Electric Angle (THETA) used for FOC according with the speed area in which the motor operates. In order to accommodate this mechanism some changes had to be made to both SLOW and FAST LOOP Subsystems.
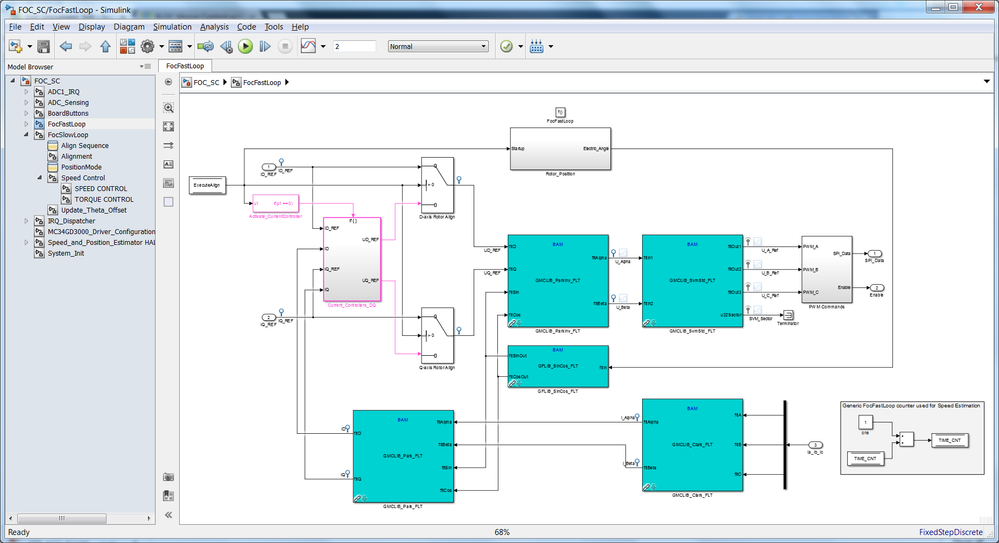 |
| Fig. 30: FAST CONTROL LOOP Simulink Model: Note the Rotor Position subsystem that computes the angle needed for PARK transformations. |
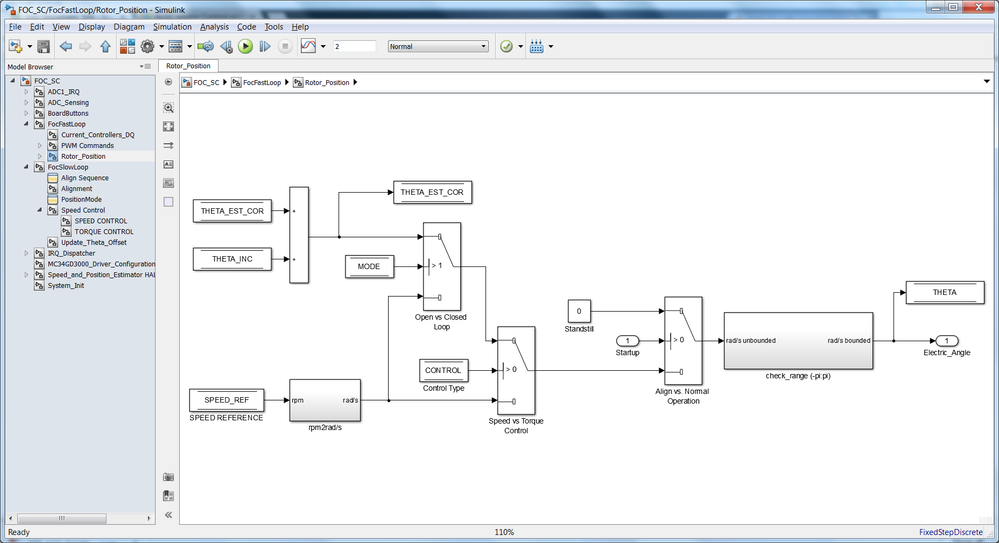 |
Fig. 31: Rotor Position Conditioning for addressing all application use-cases: - Speed Control vs. Torque Control - Open Loop vs. Closed Loop - Normal Operations vs. Rotor Alignment |
The actual speed control is implemented as normal in the slow loop using the Simulink model shown in Fig. 32.
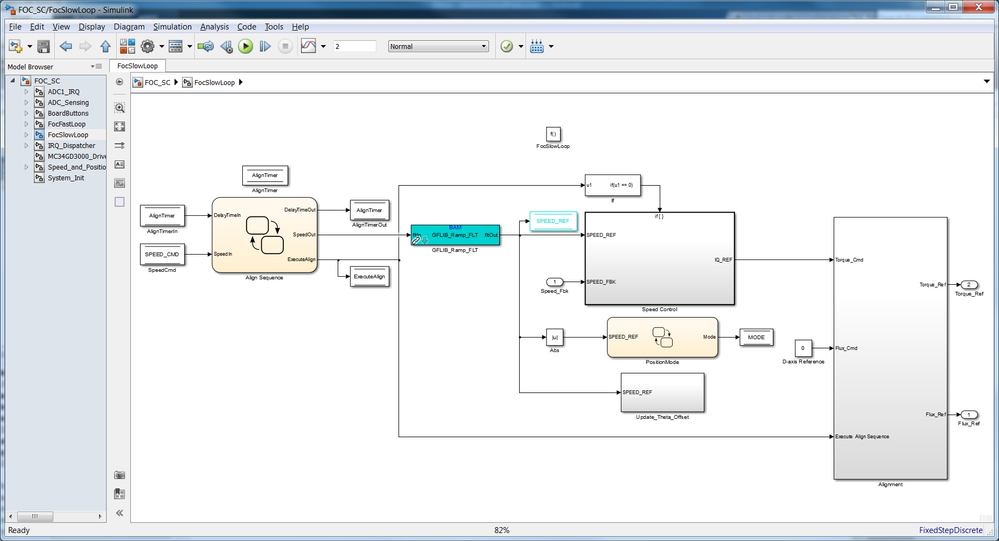 |
| Fig. 32: SLOW LOOP CONTROL Simulink Model |
The speed is regulated with the help of standard parallel form PI controller that is setting the motor torque reference IQ_REF based on the error between the SPEED_REF computed as the output of the RAMP block and the actual motor speed estimated from HALL C sensor transitions (SPEED_FBK). The controller output is limited in order to avoid a high current thru the motor and anti-windup based on clamping strategy is enabled.
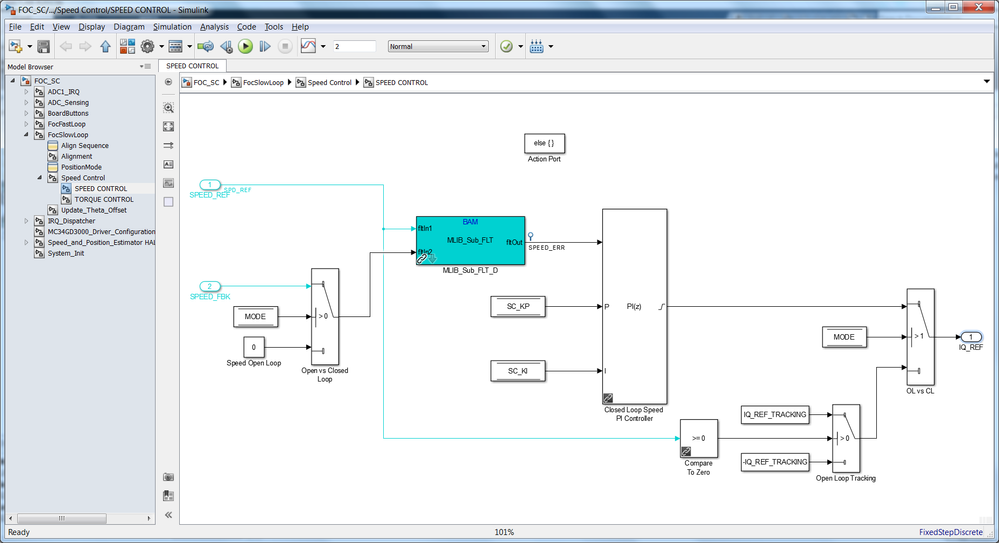 |
| Fig. 33: PI Speed Controller implementation with additional signal conditioning for handling startup and zero crossing |
The final model used for closed loop speed control is shown in Fig. 34. This model is more or less universal and represent the basic form of any speed control system based on Field Oriented Control and cascaded loops for dealing with electrical and mechanical parts of the PMSM or any motor in general.
 |
| Fig. 34: Simulink model of the Closed Loop Speed Control system for PMSM with S32K14x MCU |
RESULTS and CONCLUSIONS
The PI speed controller was tuned manually for the best results. If you prefer a more rigorous mathematical approach then you can check Motor Control Class: Lecture 11 - Closed Loop Control that explains the theory behind pole placement method starting from motor transfer function.
The next figures shows the closed loop system response under various conditions. Fig. 35 & 36 shows the system response during startup and various speed levels. Note how the PI speed controller is able to maintain the rotor speed with very good precision with a narrow band of less that +/- 100 rpm during accelerations, decelerations and steady-state regimes.
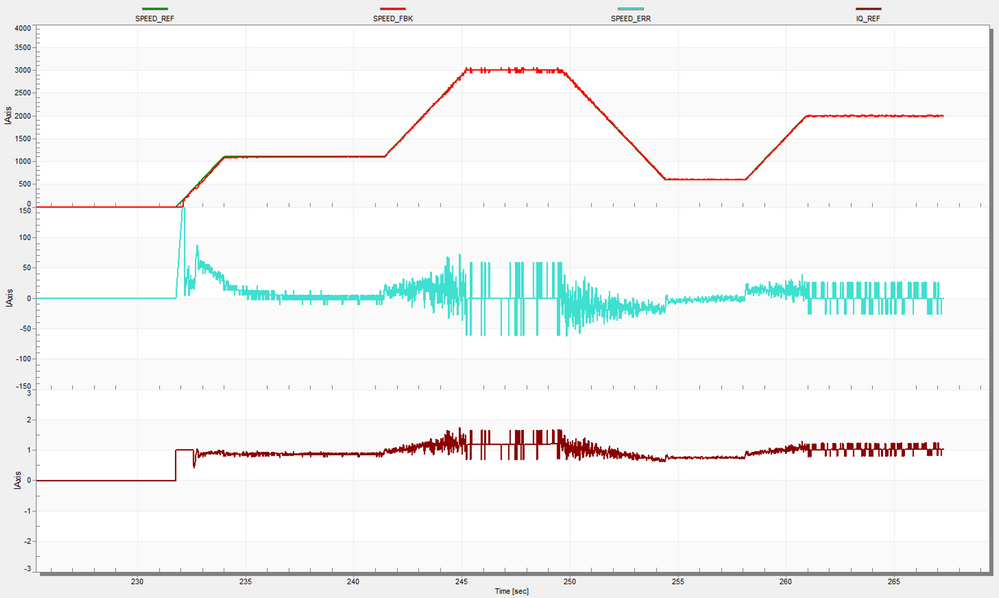 |
| Fig. 35: System startup: TOP- reference vs. actual motor speed [rpm], MIDDLE - speed error [rpm], BOTTOM - PI Speed Controller output torque reference [Amps] |
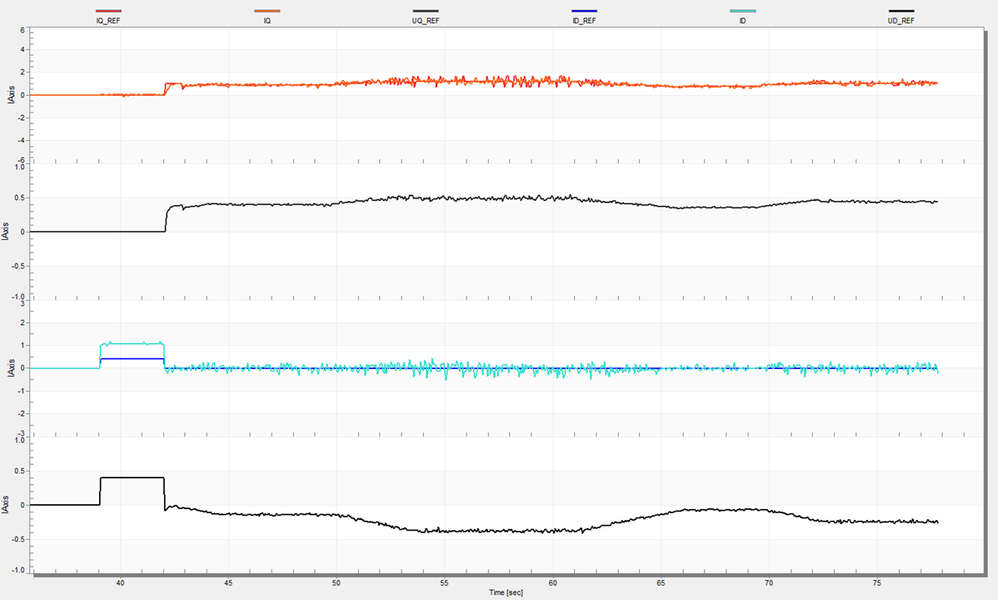 |
Fig. 36: Field Oriented Control algorithm responses for the profile shown in Fig. 36 - TOP 2 graphs: Q Axis Torque Controller inputs (IQ_REF, IQ) and output voltage command (UQ_REF) - BOTTOM 2 graphs: D Axis Flux Controller inputs (ID_REF, ID) and output voltage command (UD_REF) |
Fig. 36, demonstrates how the current controllers operates under acceleration and deceleration regimes. Note how the D-axis current controller is adjusting the control voltage in D-axis to compensate for additional back-EMF in oder to keep a zero magnetization current ID.
Fig. 37, shows the system response during startup and change of direction. Note how the handover is done between closed loop and open loop control strategies and how the rotor stops for a moment when changing directions.
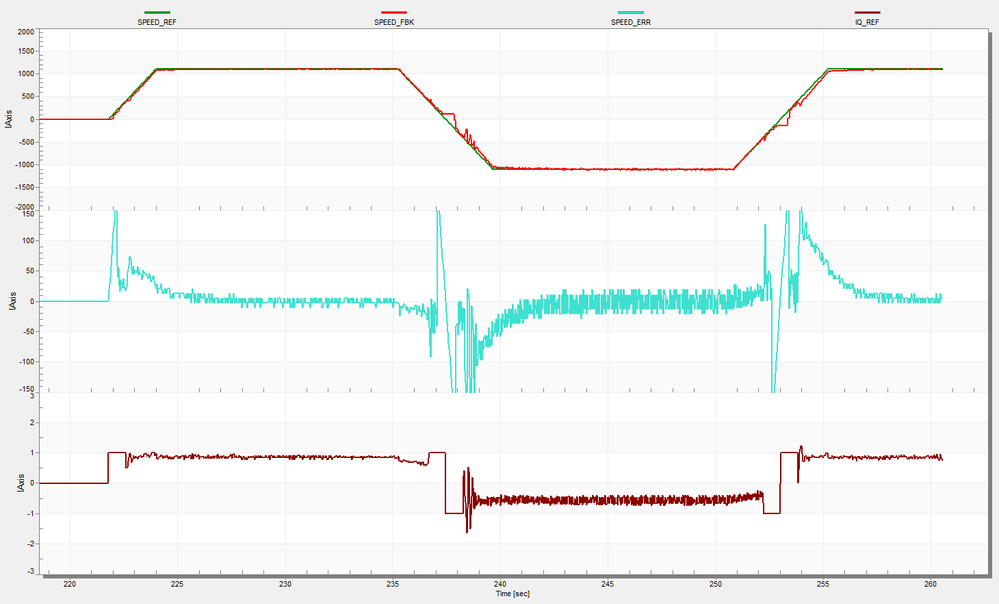 |
| Fig. 37: Motor Startup and Zero Crossing (same quantities as in Fig. 35) |
If all the results above were perform under no load conditions, the Fig. 38, shows the system response under the effect of disturbances. The motor is kept at a constant 2000 rpm speed level when suddenly random load torque are applied on the rotor shaft. The Speed Controller reacts very quickly increasing the demanded torque to compensate for the lost in speed.
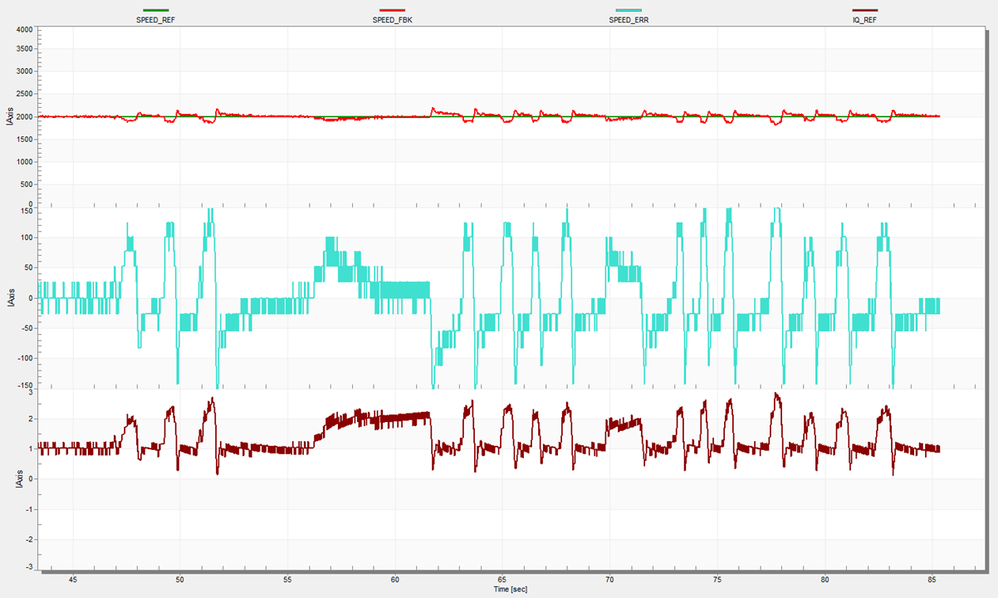 |
| Fig. 38: Speed Controller perturbation rejection |
Another interesting aspect that relates to FOC efficiency is shown in Fig. 39, where is presented the effect of phase angle compensation offset over the motor torque. By changing the value of the compensation, the motor is still able to maintain the desired speed profile within the same limits but this time with a larger current needed for producing the appropriate torque to spin the rotor. This demonstrate how important is the rotor position in FOC. A small 30 degrees deviations and the torque demanded is almost 3 times higher to maintaining the same conditions.
(a) (b) (c) |
Fig. 39: Phase angle compensation offset influence over FOC efficiency for the same speed profile and load: (a) pi/6 offset (as computed from Fig. 23 results), torque current is ~0.75Amps (b) arbitrary 15 degrees off the optimal point, torque current is ~1.2Amps (c) arbitrary 30 degrees off the optimal point, torque current is ~2.5Amps |
We hope you have found plenty of useful information in this module that will allow you to build your own speed control system.
Update revisions:
March 19, 2018
- insert a note to clarify the usage of HALL Sensors as a simple alternative for a position sensors
- update Fig. 32
- update the M8.zip model. This Simulink model is tuned for the LINIX 45ZWN24-40 motor as part of S32K144 3-phase PMSM Development Kit|NXP
- Update January 28th 2019 - This Simulink model is now available on MATLAB 2018b and MBDT for S32K14x 2018.R1 release
Before using the new models make sure you apply all the hot-patches from here: HotFix: MBD Toolbox 2018.R1 for S32K
Update revisions:
March 18, 2019
- update the model to work with Model-Based Design Toolbox for MPC57xx Automotive Version 3.0.0 .
May 06, 2020
- update the model to work with Model-Based Design Toolbox for MPC57xx Automotive Version 3.2.0 .
- Tags:
- adc
- clarke
- closed loop speed control
- devkit motor gd
- electric angle
- flux control
- foc
- hall sensors
- motor control
- motor control and power conversion
- motor control examples
- motor control on s32k
- motor controller
- motor startup
- motorgd example
- park
- permanent magnet synchronous motor
- phase delay compensation
- pi speed controller
- pmsm
- pmsm simulink model
- pmsm speed
- pmsm speed control
- position estimator
- pwm
- s32k adc
- s32k example
- s32k ftm
- s32k how to
- s32k sensors
- s32k tutorial
- s32k uart
- s32k144
- s32k144 motor control
- s32k14x
- simulink motor control
- speed control
- speed control based on hall
- speed estimator
- svm
- torque control
- zero crossing
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I have a same problem.
I downloaded M8 zip file and execute, but the motor is not spinning.
The LED is keep BLUE after blinking many times with GREEN color.
I am using same demo kit and LINIX motor.
How did you solve this problem.
I would like to know how did you solve this problem.
Thank you
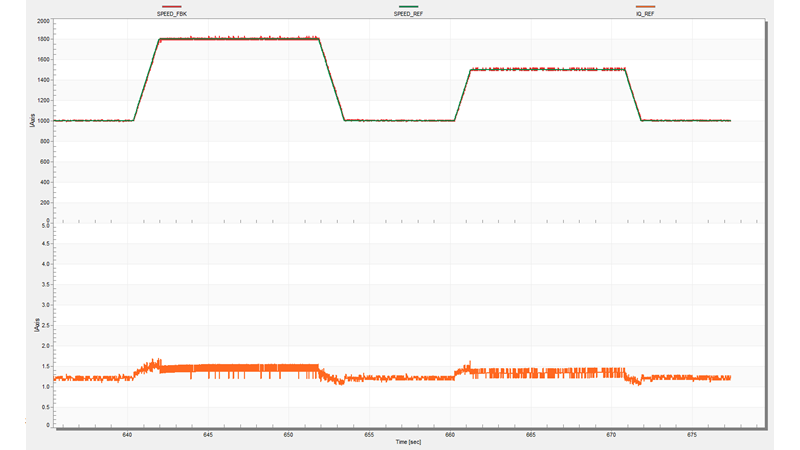
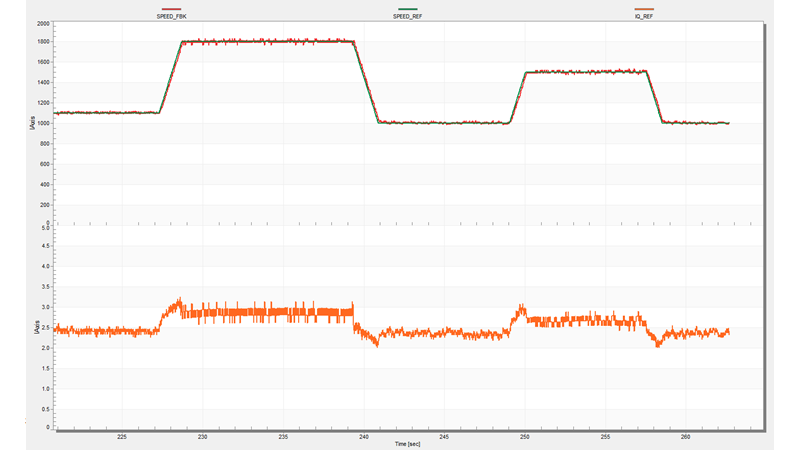
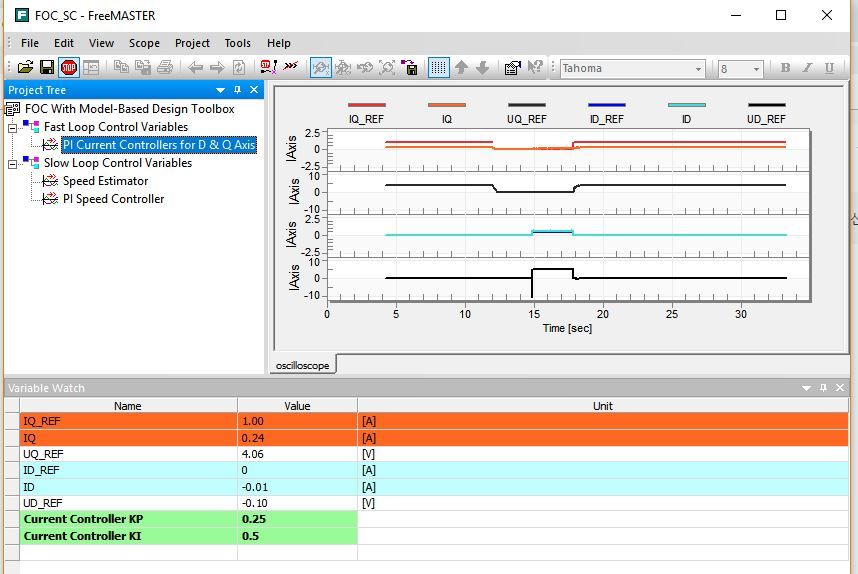
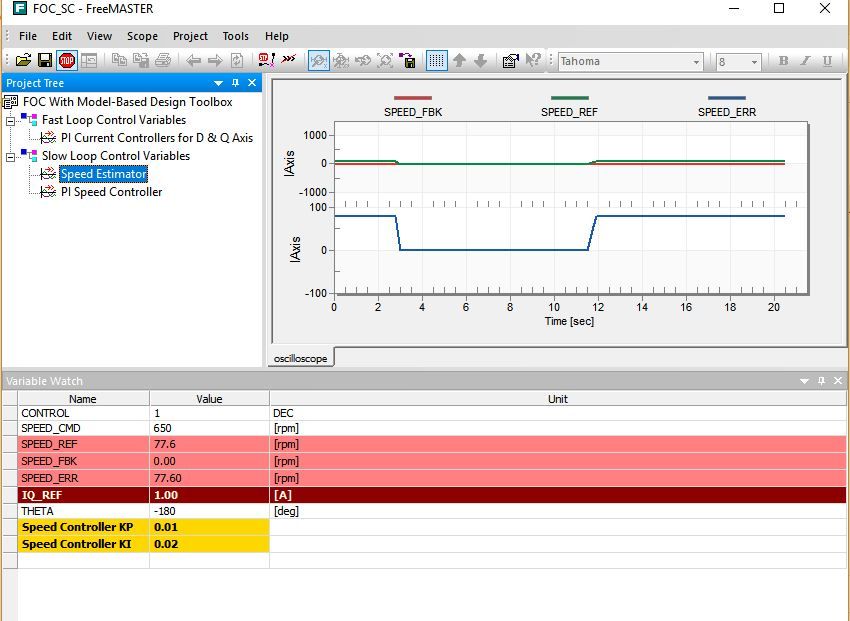
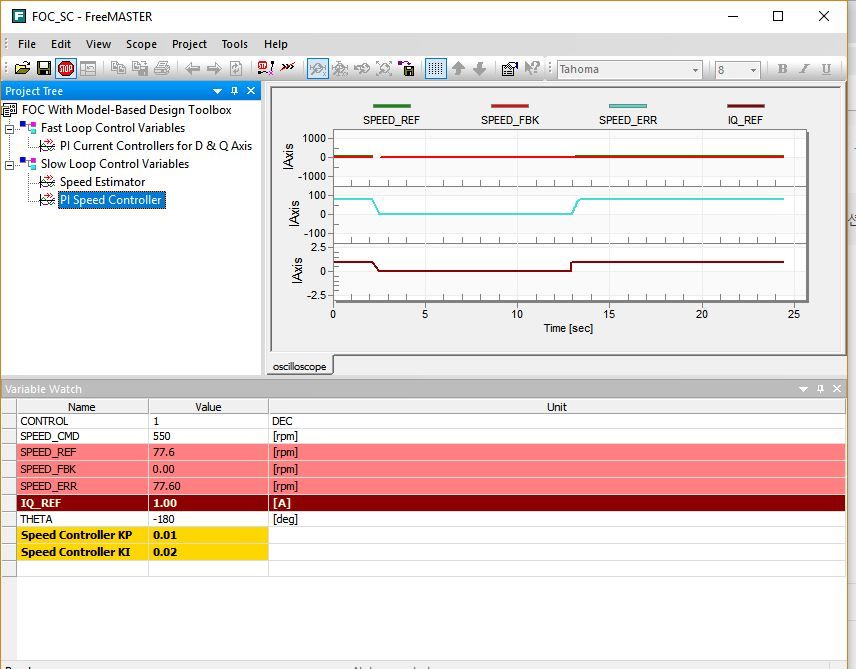
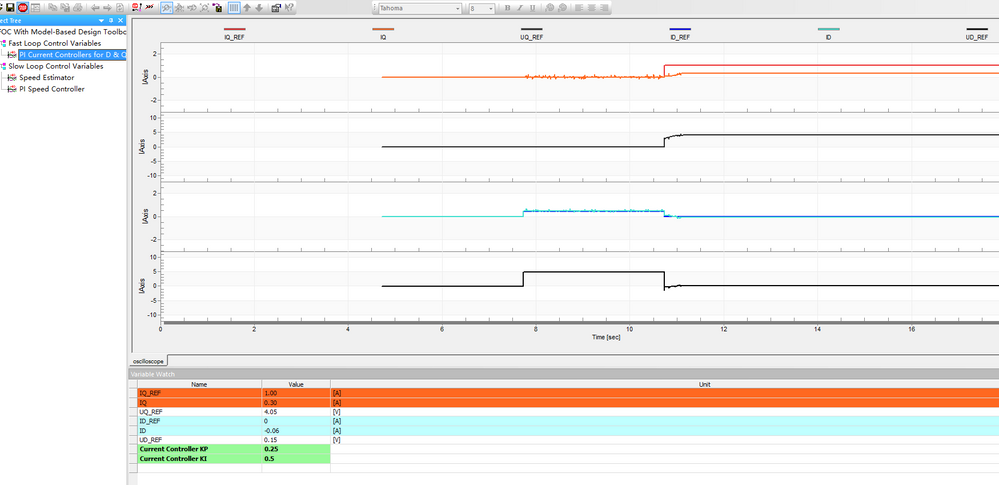
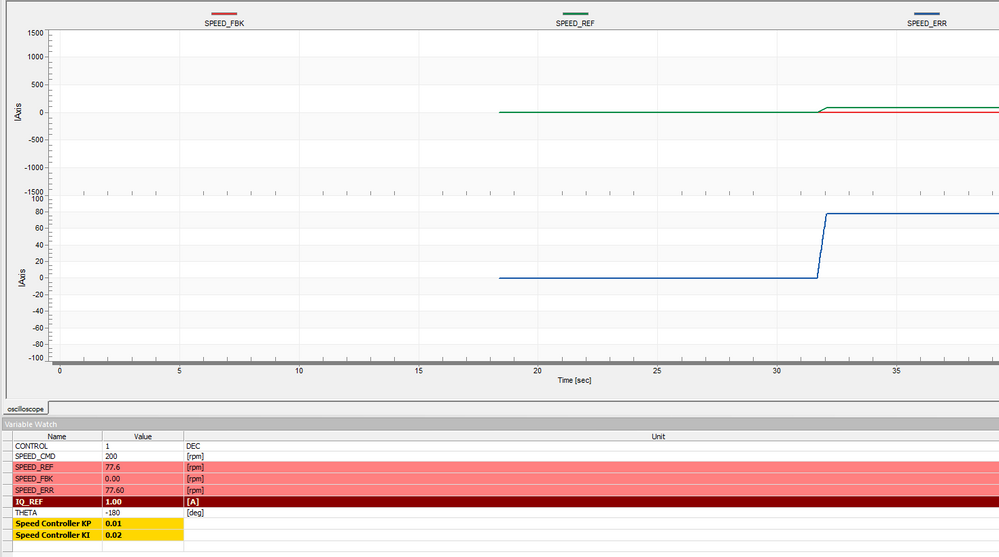
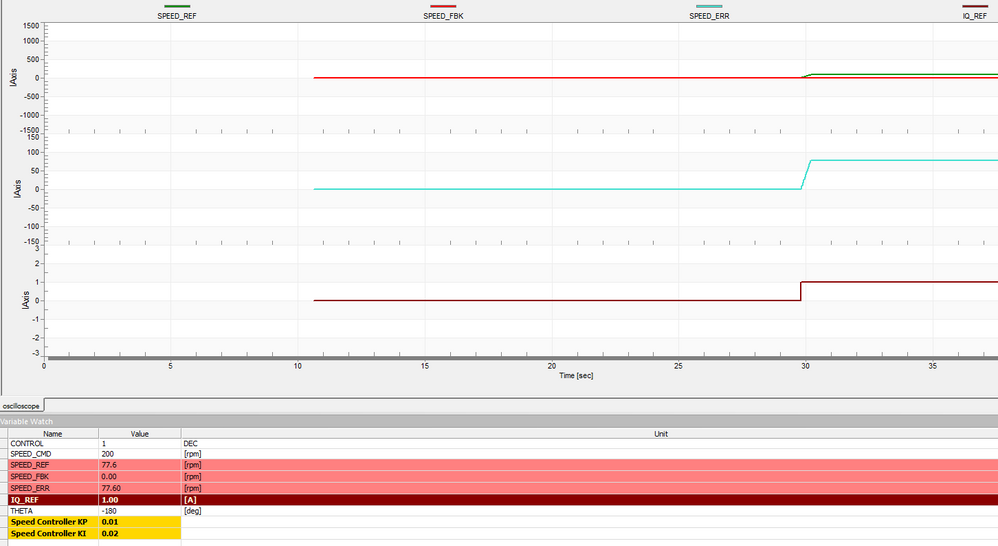
Below is my FreeMaster images
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Pony Huang,
I see that the UQREF is saturated at 0.4. Are you sure you are using the last model. Can you try by downloading once again the model attached?
Also, before starting the motor, can you try with a lower speed - let say 250rpm. Does is spin ?
Best regards,
Daniel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Daniel,
I download the model again and set SPEED_CMD at 250rpm,but the motor still does not spin.
Best regards
Pony Huang